
����Ŀ��ijУ���꼶����Ӣ���ݽ�����������A��B���ֱʼDZ���Ϊ��Ʒ�������ֱʼDZ��ĵ��۷ֱ���12Ԫ��8Ԫ�����ݱ����轱������蹺��ʼDZ���30��������������A�ʼDZ�������Ҫ������B�ʼDZ�������![]() �����ֲ�����B�ʼDZ�����
�����ֲ�����B�ʼDZ�����![]() ������A�ʼDZ�n���������ֱʼDZ����ܷ�ΪwԪ��
������A�ʼDZ�n���������ֱʼDZ����ܷ�ΪwԪ��
��1��д��w��Ԫ������n�������ĺ�����ϵʽ��������Ա���n��ȡֵ��Χ��
��2�����������ֱʼDZ�������ʱ���������٣����ٵķ����Ƕ���Ԫ��
��3���̵�Ϊ�˴�������������A�����͵ıʼDZ�ÿ������aԪ���ۣ�B�����ͱʼDZ��ۼ۲��䣮�ʹ��������ֱʼDZ������ٱ�ʱ�������٣�
���𰸡���1��5��n��![]() ����2����n=5ʱ��wȡ����СֵΪ260Ԫ����3����4��a��0����a��4ʱ��n=5������A�ʼDZ�5����B�ʼDZ�25�����������٣���4��a=0����a=4ʱ��5��n��13������A�ʼDZ�5��13����B�ʼDZ�25��17��������Ϊ240Ԫ����4��a��0����a��4ʱ��n=13������A�ʼDZ�13����B�ʼDZ�17�����������٣�
����2����n=5ʱ��wȡ����СֵΪ260Ԫ����3����4��a��0����a��4ʱ��n=5������A�ʼDZ�5����B�ʼDZ�25�����������٣���4��a=0����a=4ʱ��5��n��13������A�ʼDZ�5��13����B�ʼDZ�25��17��������Ϊ240Ԫ����4��a��0����a��4ʱ��n=13������A�ʼDZ�13����B�ʼDZ�17�����������٣�
��������
(1)��������õ�w(Ԫ)����n(��)�ĺ�����ϵʽ,�ɵõ�һ������n�IJ���ʽ��,�����n��ȡֵ��Χ,�ٽ�ϻ��ѵĺ���ʽ,�����x�ľ�����ֵ;
(2)��ϻ��ѵĺ���ʽ,�����x�ľ�����ֵ;
(3)����a��ȡֵ��Χ���ɵõ�����.
�⣺��1���������֪��w=12n+8��30��n����
��w=4n+240��
����A�ʼDZ�������Ҫ������B�ʼDZ�������![]() �����ֲ�����B�ʼDZ�������
�����ֲ�����B�ʼDZ�������![]() ��
��
��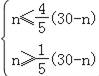 �����5��n��
�����5��n��![]() ��
��
��2��w=4n+240��
��k=4��0��
��w��n�����������
����n=5ʱ��wȡ����СֵΪ260Ԫ��
��3��w=��12��a��n+8��30��n����
��w=��4��a��n+240��
��4��a��0����a��4ʱ��n=5������A�ʼDZ�5����B�ʼDZ�25�����������٣�
��4��a=0����a=4ʱ��5��n��13������A�ʼDZ�5��13����B�ʼDZ�25��17��������Ϊ240Ԫ��
��4��a��0����a��4ʱ��n=13������A�ʼDZ�13����B�ʼDZ�17�����������٣�


 ��ѧ�����ϵ�д�
��ѧ�����ϵ�д� �·Ƿ��̸����100��ϵ�д�
�·Ƿ��̸����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��AD����ABC���ڽ�ƽ�ߣ���BC��D�㣬DE��AB��DF��AC,����ֱ�ΪE��F������EF��
��1������������������ԣ�����������ͼ�Σ�����BAC�Ľ�ƽ����ADҪ��߹���ͼ����������ͼ�ۼ�����д��������
��2���ж�AD�Ƿ�ΪEF�Ĵ�ֱƽ���ߣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Բ�桢ֱ����ͼ����д����������������ͼ�ۼ���
��֪���߶�a��
������������ABCD��ʹ��Խ���AC=a��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�P�ǵ�һ����ƽ�����ϵ�һ�㣬��P��ĺ�����Ϊ3����һ�����ǰ��ֱ�Ƕ���̶��ڵ�P�����������ǰ��Ƶ�P��ת������ת�Ĺ�������һֱ�DZ���x�ύ�ڵ�E����һֱ�DZ���y�ύ�ڵ�F������POEΪ���������Σ����F������Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
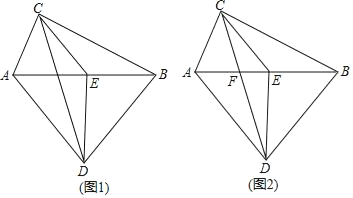
����Ŀ����ͼ����֪AC��BC��AD��BD��EΪAB���е㣬
��1����ͼ1����֤����ECD�ǵ��������Σ�
��2����ͼ2��CD��AB����ΪF����AD=BD��EF=3��DE=4����CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�������Σ�CF��BD��DF��BE����BE=BD�����CDF= �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ABC�У���C=90�㣬AC=BC��ADƽ�֡�CAB��BC��D��DE��BA��E��AB=6���ף�����DEB���ܳ���_____���ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��![]() ��˫����
��˫����![]() ����
����![]() ���㣬�ҵ�
���㣬�ҵ�![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ��
��

��1����![]() ��ֵ��
��ֵ��
��2����˫����![]() ��һ��
��һ��![]() ��������Ϊ8����
��������Ϊ8����![]() �������
�������
��3����ԭ��![]() ����һ��ֱ��
����һ��ֱ��![]() ��˫����
��˫����![]() ��
��![]() ���㣨
���㣨![]() ���ڵ�һ���ޣ������ɵ�
���ڵ�һ���ޣ������ɵ�![]() Ϊ������ɵ��ı������Ϊ
Ϊ������ɵ��ı������Ϊ![]() �����
�����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ijͬѧ�Զ���ʽ(a2��4a��2)(a2��4a��6)��4������ʽ�ֽ�Ĺ��̣�
�⣺��a2��4a��y����
ԭʽ��(y��2)(y��6)��4(��һ��)
��y2��8y��16(�ڶ���)
��(y��4)2(������)
��(a2��4a��4)2.(���IJ�)
(1)��ͬѧ��ʽ�ֽ�Ľ���Ƿף�________(����������������������)��
(2)�������ף�����ֱ��д����ʽ�ֽ���������________��
(3)����ģ�����Ϸ����Զ���ʽ(x2��2x)(x2��2x��2)��1������ʽ�ֽ⣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com