
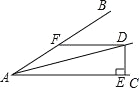
【题目】如图∠BAC=30°,D 为角平分线上一点,DE⊥AC 于 E,DF∥AC且交AB于F.
(1)求证:△ADF 是等腰三角形.
(2)若 DF=10cm,求 DE的长.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 两点,且点
两点,且点![]() 的横坐标为
的横坐标为![]() .
.

(1)求![]() 的值;
的值;
(2)若双曲线![]() 上一点
上一点![]() 的纵坐标为8,求
的纵坐标为8,求![]() 的面积;
的面积;
(3)过原点![]() 的另一条直线
的另一条直线![]() 交双曲线
交双曲线![]() 于
于![]() 两点(
两点(![]() 点在第一象限),若由点
点在第一象限),若由点![]() 为顶点组成的四边形面积为
为顶点组成的四边形面积为![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(a2-4a+2)(a2-4a+6)+4进行因式分解的过程:
解:设a2-4a=y,则
原式=(y+2)(y+6)+4(第一步)
=y2+8y+16(第二步)
=(y+4)2(第三步)
=(a2-4a+4)2.(第四步)
(1)该同学因式分解的结果是否彻底:________(填“彻底”或“不彻底”);
(2)若不彻底,请你直接写出因式分解的最后结果:________;
(3)请你模仿以上方法对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是
( )
A.![]()
B.![]()
C.5
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
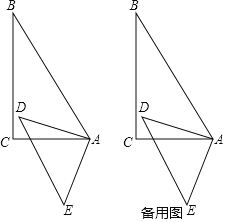
【题目】如图,将两块直角三角尺的60°角和90°角的顶点A叠放在一起.将三角尺ADE绕点A旋转,旋转过程中三角尺ADE的边AD始终在∠BAC的内部在旋转过程中,探索:
(1)∠BAE与∠CAD的度数有何数量关系,并说明理由;
(2)试说明∠CAE﹣∠BAD=30°;
(3)作∠BAD和∠CAE的平分线AM、AN,在旋转过程中∠MAN的值是否发生变化?若不变,请求出这个定值;若变化,请求出变化范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去年6月某日自治区部分市、县的最高气温(℃)如下表:
区县 | 吐鲁番 | 塔城 | 和田 | 伊宁 | 库尔勒 | 阿克苏 | 昌吉 | 呼图壁 | 鄯善 | 哈密 |
气温(℃) | 33 | 32 | 32 | 30 | 30 | 29 | 29 | 31 | 30 | 28 |
则这10个市、县该日最高气温的众数和中位数分别是( )
A.32,32
B.32,30
C.30,30
D.30,32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数学实习小组在高300米的山腰(即PH=300米)P处进行测量,测得对面山坡上A处的俯角为30°,对面山脚B处的俯角60°,已知tan∠ABC= ![]() ,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥BC,则A,B两点间的距离为米.
,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥BC,则A,B两点间的距离为米.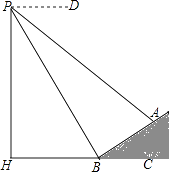
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,对角线AC与BC相交于O , E为AB的中点,F为DE的中点,G为CF的中点, OH⊥DE于H , 过A作AI⊥DE于I , 交BD于J , 交BC于K , 连接BI . 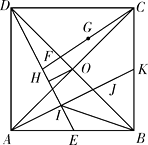
下列结论:①G到AC的距离等于 ![]() ;②OH=
;②OH= ![]() ;③BK=
;③BK= ![]() AK;④∠BIJ=45°.其中正确的结论是
AK;④∠BIJ=45°.其中正确的结论是
A.①②③
B.①②④
C.①③④
D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com