
【题目】如图,∠AOB=90°,OA=36cm,OB=12cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?

 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
【题目】某园林局有甲、乙、丙三个植树队,已知甲队植树![]() 棵,乙队植树的棵树比甲队植的棵数的2倍还多8棵,丙队植树的棵数比乙队植的棵数的一半少6棵。
棵,乙队植树的棵树比甲队植的棵数的2倍还多8棵,丙队植树的棵数比乙队植的棵数的一半少6棵。
(1)问甲队植树的棵数多还是丙队植树的棵数多?多多少棵?
(2)三个队一共植树多少棵?
(3)假设三队共植树2546棵,求三个队分别植树多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC平分∠DAB,CE⊥AB于E,AB=AD+2BE,则下列结论:①AB+AD=2AE;②∠DAB+∠DCB=180°;③CD=CB;④S△ACE﹣2S△BCE=S△ADC;其中正确结论的个数是( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是学生小金家附近的一块三角形绿化区的示意图,为增强体质,他每天早晨都沿着绿化区周边小路AB、BC、CA跑步
是学生小金家附近的一块三角形绿化区的示意图,为增强体质,他每天早晨都沿着绿化区周边小路AB、BC、CA跑步![]() 小路的宽度不计
小路的宽度不计![]() 观测得点B在点A的南偏东
观测得点B在点A的南偏东![]() 方向上,点C在点A的南偏东
方向上,点C在点A的南偏东![]() 的方向上,点B在点C的北偏西
的方向上,点B在点C的北偏西![]() 方向上,AC间距离为400米
方向上,AC间距离为400米![]() 问小金沿三角形绿化区的周边小路跑一圈共跑了多少米?
问小金沿三角形绿化区的周边小路跑一圈共跑了多少米?
![]() 参考数据:
参考数据:![]() ,
,![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,有若干个点按如下规律排列:(1,1),(2,1),(2,2),(3,1),(3,2),(3,3),…,则第100个点的横坐标为( )

A.12B.13C.14D.15
查看答案和解析>>
科目:初中数学 来源: 题型:
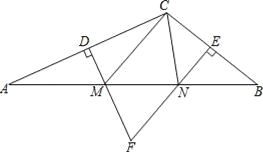
【题目】如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N两点,DM与EN相交于点F.
(1)若△CMN的周长为15cm,求AB的长;
(2)若∠MFN=70°,求∠MCN的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AM∥BN,∠B=40°,点P是BN上一动点(与点B不重合).AC、AD分别平分∠BAP和∠PAM,交射线BN于点C、D.

(1)求∠CAD的度数;
(2)当点P运动到当∠ACB=∠BAD时,求∠BAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠C=90°,∠A=34°,D,E 分别为 AB,AC 上一点,将△BCD,△ADE 沿 CD,DE 翻折,点 A,B 恰好重合于点 P 处,则∠ACP=_______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某经销商经销的学生用品,他以每件280元的价格购进某种型号的学习机,以每件360元的售价销售时,每月可售出60个,为了扩大销售,该经销商采取降价的方式促销,在销售中发现,如果每个学习机降价1元,那么每月就可以多售出5个.
![]() 降价前销售这种学习机每月的利润是多少元?
降价前销售这种学习机每月的利润是多少元?
![]() 经销商销售这种学习机每月的利润要达到7200元,且尽可能让利于顾客,求每个学习机应降价多少元?
经销商销售这种学习机每月的利润要达到7200元,且尽可能让利于顾客,求每个学习机应降价多少元?
![]() 在
在![]() 的销售中,销量可好,经销商又开始涨价,涨价后每月销售这种学习机的利润能达到10580元吗?若能,请求出涨多少元;若不能,请说明理由.
的销售中,销量可好,经销商又开始涨价,涨价后每月销售这种学习机的利润能达到10580元吗?若能,请求出涨多少元;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com