
【题目】如图,已知AC平分∠DAB,CE⊥AB于E,AB=AD+2BE,则下列结论:①AB+AD=2AE;②∠DAB+∠DCB=180°;③CD=CB;④S△ACE﹣2S△BCE=S△ADC;其中正确结论的个数是( )

A.1个B.2个C.3个D.4个
【答案】C
【解析】
①在AE取点F,使EF=BE.利用已知条件AB=AD+2BE,可得AD=AF,进而证出2AE=AB+AD;
②在AB上取点F,使BE=EF,连接CF.先由SAS证明△ACD≌△ACF,得出∠ADC=∠AFC;再根据线段垂直平分线、等腰三角形的性质得出∠CFB=∠B;然后由邻补角定义及四边形的内角和定理得出∠DAB+∠DCB=180°;
③根据全等三角形的对应边相等得出CD=CF,根据线段垂直平分线的性质得出CF=CB,从而CD=CB;
④由于△CEF≌△CEB,△ACD≌△ACF,根据全等三角形的面积相等易证S△ACE-S△BCE=S△ADC.
解:①在AE取点F,使EF=BE,
∵AB=AD+2BE=AF+EF+BE,EF=BE,
∴AB=AD+2BE=AF+2BE,
∴AD=AF,
∴AB+AD=AF+EF+BE+AD=2AF+2EF=2(AF+EF)=2AE,
∴AE=![]() (AB+AD),故①正确;
(AB+AD),故①正确;
②在AB上取点F,使BE=EF,连接CF.
在△ACD与△ACF中,∵AD=AF,∠DAC=∠FAC,AC=AC,
∴△ACD≌△ACF,
∴∠ADC=∠AFC.
∵CE垂直平分BF,
∴CF=CB,
∴∠CFB=∠B.
又∵∠AFC+∠CFB=180°,
∴∠ADC+∠B=180°,
∴∠DAB+∠DCB=360-(∠ADC+∠B)=180°,故②正确;
③由②知,△ACD≌△ACF,∴CD=CF,
又∵CF=CB,
∴CD=CB,故③正确;
④易证△CEF≌△CEB,
所以S△ACE-S△BCE=S△ACE-S△FCE=S△ACF,
又∵△ACD≌△ACF,
∴S△ACF=S△ADC,
∴S△ACE-S△BCE=S△ADC,故④错误;
即正确的有3个,
故选:C.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点A在原点,B、C坐标分别为B(3,0),C(2,2),将△ABC向左平移1个单位后再向下平移2单位,可得到△A′B′C′.

(1)请画出平移后的△ABC的图形
(2)写出△A′B′C′各个顶点的坐标;
(3)在x轴上是否存在点P,值![]() ,若存在,请写出P点的坐标,若不存在请说明理由.
,若存在,请写出P点的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里装有4个小球,分别标有数字1,2,3,4;这些小球除所标数字不同外,其余完全相同,甲乙两人每次同时从袋中各随机摸出一个小球,记下球上的数字,并计算它们的积.
![]() 请用画树状图或列表的方法,求两数积是8的概率;
请用画树状图或列表的方法,求两数积是8的概率;
![]() 甲乙两人想用这种方式做游戏,他们规定,当两数之积是偶数时,甲得1分,当两数之积是奇数时,乙得3分,你认为这个游戏公平吗?请说明理由,若你认为不公平,请修改得分规则,使游戏公平.
甲乙两人想用这种方式做游戏,他们规定,当两数之积是偶数时,甲得1分,当两数之积是奇数时,乙得3分,你认为这个游戏公平吗?请说明理由,若你认为不公平,请修改得分规则,使游戏公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OC是∠AOB的角平分线,P是OC上一点.PD⊥OA交OA于D,PE⊥OB交OB于E,F是OC上的另一点,连接DF,EF.求证:DF=EF.
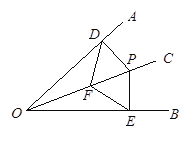
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山地自行车越来越受到中学生的喜爱,各种品牌相继投放市场,某车行经营的A型车去年销售总额为5万元,今年每辆销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.
(1)今年A型车每辆售价多少元?(用列方程的方法解答)
(2)该车行计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A,B两种型号车的进货和销售价格如下表:
A型车 | B型车 | |
进货价格(元) | 1100 | 1400 |
销售价格(元) | 今年的销售价格 | 2000 |
查看答案和解析>>
科目:初中数学 来源: 题型:
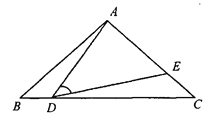
【题目】如图,在△ABC中,AB=AC=9,BC=12,∠B=∠C,点D从B出发以每秒2厘米的速度在线段BC上从B向C方向运动,点E同时从C出发以每秒2厘米的速度在线段AC上从C向A运动,连接AD、DE.
(1)运动 秒时,AE=![]() DC(不必说明理由)
DC(不必说明理由)
(2)运动多少秒时,∠ADE=90°-![]() ∠BAC,并请说明理由;
∠BAC,并请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,OA=36cm,OB=12cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知两条直线AB,CD被直线EF所截,分别交于点E,点F,EM平分∠AEF交CD于点M,且∠FEM=∠FME.

(1)直线AB与直线CD是否平行,说明你的理由;
(2)如图2,点G是射线MD上一动点(不与点M,F重合),EH平分∠FEG交CD于点H,过点H作HN⊥EM于点N,设∠EHN=α,∠EGF=β.
①当点G在点F的右侧时,若β=60°,求α的度数;
②当点G在运动过程中,α和β之间有怎样的数量关系?请写出你的猜想,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com