
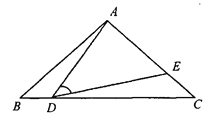
【题目】如图,在△ABC中,AB=AC=9,BC=12,∠B=∠C,点D从B出发以每秒2厘米的速度在线段BC上从B向C方向运动,点E同时从C出发以每秒2厘米的速度在线段AC上从C向A运动,连接AD、DE.
(1)运动 秒时,AE=![]() DC(不必说明理由)
DC(不必说明理由)
(2)运动多少秒时,∠ADE=90°-![]() ∠BAC,并请说明理由;
∠BAC,并请说明理由;
【答案】(1)3;(2)运动![]() 秒时,∠ADE=90°
秒时,∠ADE=90°![]() ∠BAC.
∠BAC.
【解析】
(1)设运动的时间是t秒,则CD=12-2t,AE=9-2t,得出方程9-2t=![]() (12-2t),求出方程的解即可;(2)求出∠B=∠C=∠ADE,推出∠BAD=∠EDC,根据AAS证△ABD≌△DCE,推出DC=AB=9即可.
(12-2t),求出方程的解即可;(2)求出∠B=∠C=∠ADE,推出∠BAD=∠EDC,根据AAS证△ABD≌△DCE,推出DC=AB=9即可.
(1)设运动的时间是t秒,
则CD=122t,AE=92t,
92t=![]() (122t)
(122t)
t=3,
故答案为:3.
(2)设x秒后,∠ADE=90°![]() ∠BAC,
∠BAC,
∵∠B=∠C=90°![]() ∠BAC,
∠BAC,
∴∠B=∠C=∠ADE,
∵∠BAD+∠ADB+∠B=180°,∠EDC+∠ADE+∠ADB=180°,
∴∠BAD=∠EDC,
在△ABD和△DCE中,
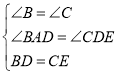
∴△ABD≌△DCE(AAS),
∴DC=AB=9,
∴BD=3,
∴x=![]() ,
,
即运动![]() 秒时,∠ADE=90°
秒时,∠ADE=90°![]() ∠BAC.
∠BAC.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.
求证:四边形ADCF是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
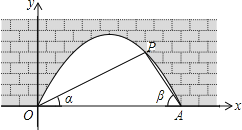
【题目】图中是抛物线拱桥,P处有一照明灯,点P到水面OA的距离为![]() ,从O、A两处观测P处,仰角分别为
,从O、A两处观测P处,仰角分别为![]() ,
,![]() ,且
,且![]() ,
,![]() ,以O为原点,OA所在直线为x轴建立直角坐标系,已知抛物线方程为
,以O为原点,OA所在直线为x轴建立直角坐标系,已知抛物线方程为![]() .
.
![]() 求抛物线方程,并求抛物线上的最高点到水面的距离;
求抛物线方程,并求抛物线上的最高点到水面的距离;
![]() 水面上升1m,水面宽多少
水面上升1m,水面宽多少![]() 取
取![]() ,结果精确到
,结果精确到![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC平分∠DAB,CE⊥AB于E,AB=AD+2BE,则下列结论:①AB+AD=2AE;②∠DAB+∠DCB=180°;③CD=CB;④S△ACE﹣2S△BCE=S△ADC;其中正确结论的个数是( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雾霾天气持续笼罩我国大部分地区,困扰着广大市民的生活,口罩市场出现热销,小明的爸爸用12000元购进甲、乙两种型号的口罩在自家商店销售,销售完后共获利2700元,进价和售价如表:

(1)小明爸爸的商店购进甲、乙两种型号口罩各多少袋?
(2)该商店第二次以原价购进甲、乙两种型号口罩,购进甲种型号口罩袋数不变,而购进乙种型号口罩袋数是第一次的2倍,甲种口罩按原售价出售,而效果更好的乙种口罩打折让利销售,若两种型号的口罩全部售完,要使第二次销售活动获利不少于2460元,每袋乙种型号的口罩最多打几折?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是学生小金家附近的一块三角形绿化区的示意图,为增强体质,他每天早晨都沿着绿化区周边小路AB、BC、CA跑步
是学生小金家附近的一块三角形绿化区的示意图,为增强体质,他每天早晨都沿着绿化区周边小路AB、BC、CA跑步![]() 小路的宽度不计
小路的宽度不计![]() 观测得点B在点A的南偏东
观测得点B在点A的南偏东![]() 方向上,点C在点A的南偏东
方向上,点C在点A的南偏东![]() 的方向上,点B在点C的北偏西
的方向上,点B在点C的北偏西![]() 方向上,AC间距离为400米
方向上,AC间距离为400米![]() 问小金沿三角形绿化区的周边小路跑一圈共跑了多少米?
问小金沿三角形绿化区的周边小路跑一圈共跑了多少米?
![]() 参考数据:
参考数据:![]() ,
,![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,有若干个点按如下规律排列:(1,1),(2,1),(2,2),(3,1),(3,2),(3,3),…,则第100个点的横坐标为( )

A.12B.13C.14D.15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AM∥BN,∠B=40°,点P是BN上一动点(与点B不重合).AC、AD分别平分∠BAP和∠PAM,交射线BN于点C、D.

(1)求∠CAD的度数;
(2)当点P运动到当∠ACB=∠BAD时,求∠BAC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com