
【题目】如图,若BC=EC,∠BCE=∠ACD,则添加不能使△ABC≌△DBC的条件是( )

A.AB=DE B.∠B=∠E C.AC=DC D.∠A=∠D
【答案】A.
【解析】
试题分析:先求出∠ACB=∠DCE,再根据全等三角形的判定定理(SAS,ASA,AAS,SSS)逐个判断即可.
解:∵∠BCE=∠ACD,
∴∠BCE+∠ACE=∠ACD+∠ACE,
∴∠ACB=∠DCE,
A、根据BC=CE,AB=DE,∠ACB=∠DCE不能推出△ABC≌△DEC,故本选项正确;
B、因为∠ACB=∠DCE,∠B=∠E,BC=CE,所以符合AAS定理,即能推出△ABC≌△DEC,故本选项错误;
C、因为BC=CE,∠ACB=∠DCE,AC=CD,所以符合SAS定理,即能推出△ABC≌△DEC,故本选项错误;
D、因为∠A=∠D,∠ACB=∠DCE,BC=CE,所以符合AAS定理,即能推出△ABC≌△DEC,故本选项错误;
故选A.


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】为了提高饮水质量,越来越多的居民开始选购家用净水器.一商场抓住商机,从厂家购进了A、B两种净水器共160台,A型家用净水器的进价是每台150元,B型净水器的进价是每台350元,购进两种净水器共用去了36000元。
(1)求A、B两种净水器各购进了多少台?
(2)为使每台B型净水器的毛利润是A型净水器的2倍,且保证售完这160台净水器的毛利润不低于11000元,求每台A型净水器的售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
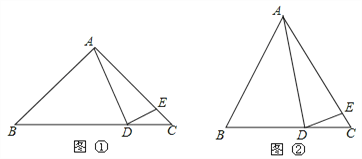
【题目】(14分)探究与发现:如图①,在Rt△ABC中,∠BAC=90°,AB=AC,点D在底边BC上,AE=AD,连结DE.
(1)当∠BAD=60°时,求∠CDE的度数;
(2)当点D在BC (点B、C除外) 上运动时,试猜想并探究∠BAD与∠CDE的数量关系;
(3)深入探究:若∠BAC≠90°,试就图②探究∠BAD与∠CDE的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作与实践:已知长方形纸片ABCD中,AD=3,AB=4.
操作一:如图①,任意画一条线段EF,将纸片沿EF折叠,使点B落到点B′的位置,EB′与CD交于点G.试说明重叠部分△EFG为等腰三角形;
操作二:如图②,将纸片沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点H.求△B′HC的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(﹣a)7÷(﹣a)4×(﹣a)3
(2)a3(﹣b3)2+(﹣2ab2)3
(3)2(a2)3﹣a2![]() a4+(2a4)2÷a2
a4+(2a4)2÷a2
(4)(![]() )﹣3﹣(3.14﹣π)0+(﹣2)4.
)﹣3﹣(3.14﹣π)0+(﹣2)4.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ΔABC和ΔDEF中,已知∠C=∠D,∠B=∠E,要判断这两个三角形全等,还需添加条件( )
A. AB=ED B. AB=FD C. AC=FD D. ∠A =∠F.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com