
【题目】操作与实践:已知长方形纸片ABCD中,AD=3,AB=4.
操作一:如图①,任意画一条线段EF,将纸片沿EF折叠,使点B落到点B′的位置,EB′与CD交于点G.试说明重叠部分△EFG为等腰三角形;
操作二:如图②,将纸片沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点H.求△B′HC的周长.

【答案】(1)证明见解析(2)7.
【解析】
试题分析:(1)由矩形的性质可知DC∥AB,根据平行线的性质可知∠GFE=∠FEB,由翻折的性质可知∠GEF=∠BEF,从而得到∠FEB=∠BEF从而得到三角形EFG为等腰三角形;
(2)先证明△ADH≌△CB′H,从而得到DH=DB′,然后将△B′HC的周长转化为三角形B′C与DC的和即可.
解:(1)由折叠的性质可知∠GEF=∠BEF.
∵DC∥AB,
∴∠GFE=∠FEB.
∴∠FEB=∠BEF.
∴EG=FG.
∴△EFG为等腰三角形.
(2)∵四边形ABCD为矩形,
∴AD=BC.
由翻折的性质可知:BC=CB′,∠B′=∠B=90°.
∴AD=CB′,∠D=∠B′.
在△ADH和△CB′H中,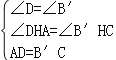 ,
,
∴△ADH≌△CB′H.
∴B′H=DH.
∴△B′HC的周长=B′C+B′H+HC=BC+DH+HC=7.


科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
①b2>4ac;
②4a﹣2b+c<0;
③不等式ax2+bx+c>0的解集是x≥3.5;
④若(﹣2,y1),(5,y2)是抛物线上的两点,则y1<y2.
上述4个判断中,正确的是( )
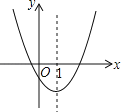
A.①② B.①④ C.①③④ D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,平方数的开平方运算可以直接求得,如![]() 等,有些数则不能直接求得,如
等,有些数则不能直接求得,如![]() ,但可以通过计算器求得.还有一种方法可以通过一组数的内在联系,运用规律求得.请你观察下表:
,但可以通过计算器求得.还有一种方法可以通过一组数的内在联系,运用规律求得.请你观察下表:
a … 0.04 4 400 40000 …
![]() … x 2 y z …
… x 2 y z …
(1)表格中的三个值分别为:x= ;y= ;z= ;
(2)用公式表示这一规律:当a=4×100n(n为整数)时,![]() = ;
= ;
(3)利用这一规律,解决下面的问题:
已知![]() ≈2.358,则①
≈2.358,则①![]() ≈ ;②
≈ ;②![]() ≈ .
≈ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若BC=EC,∠BCE=∠ACD,则添加不能使△ABC≌△DBC的条件是( )

A.AB=DE B.∠B=∠E C.AC=DC D.∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
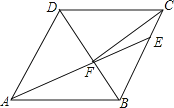
【题目】如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,CE=2,连接CF,以下结论:①△ABF≌△CBF;②点E到AB的距离是2![]() ;③tan∠DCF=
;③tan∠DCF=![]() ;④△ABF的面积为
;④△ABF的面积为![]()
![]() .其中一定成立的是 (把所有正确结论的序号都填在横线上).
.其中一定成立的是 (把所有正确结论的序号都填在横线上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:
①全等三角形的形状相同、大小相等
②全等三角形的对应边相等、对应角相等
③面积相等的两个三角形全等
④全等三角形的周长相等
其中正确的说法为( )
A.①②③④ B.①②③ C.②③④ D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在元旦联欢会上,3名小朋友分别站在△ABC三个顶点的位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先做到凳子上谁获胜,为使游戏公平,则凳子应放置的最适当的位置时在△ABC的( )
A. 三边垂直平分线的交点 B. 三条角平分线的交点
C. 三边中线的交点 D. 三边上高的交点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com