
【题目】如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE,∠AOD:∠BOD=2:1 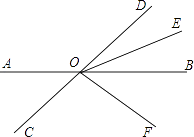
(1)求∠DOE的度数;
(2)求∠AOF的度数.
【答案】
(1)解:∵∠AOD:∠BOD=2:1,∠AOD+∠BOD=180°,
∴∠BOD= ![]() ×180°=60°,
×180°=60°,
∵OE平分∠BOD,
∴∠DOE= ![]() ∠BOD=
∠BOD= ![]() ×60°=30°
×60°=30°
(2)解:∠COE=∠COD﹣∠DOE=180°﹣30°=150°,
∵OF平分∠COE,
∴∠COF= ![]() ∠COE=
∠COE= ![]() ×150°=75°,
×150°=75°,
∵∠AOC=∠BOD=60°(对顶角相等),
∴∠AOF=∠AOC+∠COF=60°+75°=135°
【解析】(1)根据邻补角的和等于180°求出∠BOD的度数,然后根据角平分线的定义解答;(2)先求出∠COE的度数,再根据角平分线的定义求出∠COF,然后根据对顶角相等求出∠AOC,再根据∠AOF=∠AOC+∠COF,代入数据进行计算即可得解.
【考点精析】关于本题考查的角的平分线和对顶角和邻补角,需要了解从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】有理数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( ) ![]()
A.a>b
B.|a﹣c|=a﹣c
C.﹣a<﹣b<c
D.|b+c|=b+c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育老师对甲、乙两名同学分别进行了8次跳高测试,经计算这两名同学成绩的平均数相同,甲同学的方差是S甲2=6.4,乙同学的方差是S乙2=8.2,那么这两名同学跳高成绩比较稳定的是同学.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下四个命题:
①若一个角的两边和另一个角的两边分别互相垂直,则这两个角互补;
②边数相等的两个正多边形一定相似;
③等腰三角形ABC中,D是底边BC上一点,E是一腰AC上的一点,若∠BAD=60°且AD=AE,则∠EDC=30°;
④任意三角形的外接圆的圆心一定是三角形三条边的垂直平分线的交点.
其中正确命题的序号为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
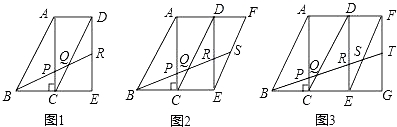
【题目】现有多个全等直角三角形,先取三个拼成如图1所示的形状,R为DE的中点,BR分别交AC,CD于P,Q,易得BP:QP:QR=3:1:2.
(1)若取四个直角三角形拼成如图2所示的形状,S为EF的中点,BS分别交AC,CD,DE于P,Q,R,则BP:PQ:QR:RS=
(2)若取五个直角三角形拼成如图3所示的形状,T为FG的中点,BT分别交AC,CD,DE,EF于P,Q,R,S,则BP:PQ:QR:RS:ST= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把△ABC纸片沿DE折叠,当点A在四边形BCDE的外部时,记∠AEB为∠1,∠ADC为∠2,则∠A、∠1与∠2的数量关系,结论正确的是( )

A. ∠1=∠2+∠A B. ∠1=2∠A+∠2
C. ∠1=2∠2+2∠A D. 2∠1=∠2+∠A
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+2![]() =(1+
=(1+![]() )2.善于思考的小明进行了以下探索:
)2.善于思考的小明进行了以下探索:
设a+b![]() =(m+n
=(m+n![]() )2(其中a、b、m、n均为整数),则有a+b
)2(其中a、b、m、n均为整数),则有a+b![]() =m2+2n2+2mn
=m2+2n2+2mn![]() .
.
∴a=m2+2n2,b=2mn.这样小明就找到了一种把类似a+b![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b![]() =
=![]() ,用含m、n的式子分别表示a、b,得:a=__,b=__;
,用含m、n的式子分别表示a、b,得:a=__,b=__;
(2)利用所探索的结论,找一组正整数a、b、m、n填空:__+__![]() =(___)+__
=(___)+__![]() )2;
)2;
(3)若a+4![]() =
=![]() ,且a、m、n均为正整数,求a的值?
,且a、m、n均为正整数,求a的值?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com