
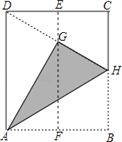
【题目】如图,在一张矩形纸片ABCD中,AD=4cm,点E,F分别是CD和AB的中点,现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH,若HG延长线恰好经过点D,则CD的长为_________.
【答案】![]()
【解析】试题分析:先证明EG是△DCH的中位线,继而得出DG=HG,然后证明△ADG≌△AHG,得出∠BAH=∠HAG=∠DAG=30°,在Rt△ABH中,可求出AB,也即是CD的长.
试题解析:∵点E,F分别是CD和AB的中点,
∴EF⊥AB,
∴EF∥BC,
∴EG是△DCH的中位线,
∴DG=HG,
由折叠的性质可得:∠AGH=∠ABH=90°,
∴∠AGH=∠AGD=90°,
在△AGH和△AGD中,
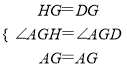
∴△ADG≌△AHG(SAS),
∴AD=AH,∠DAG=∠HAG,
由折叠的性质可得:∠BAH=∠HAG,
∴∠BAH=∠HAG=∠DAG=![]() ∠BAD=30°,
∠BAD=30°,
在Rt△ABH中,AH=AD=4,∠BAH=30°,
∴HB=2,AB=2![]() ,
,
∴CD=AB=2![]() .
.


科目:初中数学 来源: 题型:
【题目】如图所示,PA,PB是⊙O的两条切线,A,B为切点,连接PO,交⊙O于点D,交AB于点C,
(1)写出圆中所有的垂直的关系;
(2)若PA=4,PD=2,求半径OA的长;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,∠B=60°,△ADE可以由△ABC绕点 A顺时针旋转900得到,点D 与点B是对应点,点E与点C是对应点,连接CE,则∠CED的度数是( )

A. 45° B. 30° C. 25° D. 15°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,线段![]() 和射线
和射线![]() 交于点
交于点![]() .
.
(![]() )利用尺规完成以下作图,并保留作图痕迹(不写作法).
)利用尺规完成以下作图,并保留作图痕迹(不写作法).
①在射线![]() 上作一点
上作一点![]() ,使
,使![]() ,连接
,连接![]() ;
;
②作![]() 的角平分线交
的角平分线交![]() 于
于![]() 点;
点;
③在射线![]() 上作一点
上作一点![]() ,使
,使![]() ,连接
,连接![]() .
.
(![]() )在(
)在(![]() )所作的图形中,通过观察和测量可以发现
)所作的图形中,通过观察和测量可以发现![]() ,请将下面的证明过程补充完整.
,请将下面的证明过程补充完整.

证明:∵![]() ,
,
∴![]() __________
__________![]() __________,①
__________,①
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() __________,②
__________,②
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .( )
.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要从甲.乙两名同学中选出一名,代表班级参加射击比赛,如图是两人最近10次射击训练成绩的折线统计图.
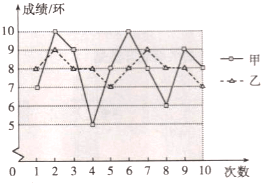
(1)已求得甲的平均成绩为8环,求乙的平均成绩;
(2)观察图形,直接写出甲,乙这10次射击成绩的方差![]() ,
, ![]() 哪个大;
哪个大;
(3)如果其他班级参赛选手的射击成绩都在7环左右,本班应该选 参赛更合适;如果其他班级参赛选手的射击成绩都在9环左右,本班应该选 参赛更合适.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年2班组织了一次经典诵读比赛,甲乙两组各10人的比赛成绩如下表(10分制):

(I)甲组数据的中位数是 ,乙组数据的众数是 ;
(Ⅱ)计算乙组数据的平均数和方差;
(Ⅲ)已知甲组数据的方差是1.4分2,则成绩较为整齐的是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,学校准备在教学楼后面搭建一简易矩形自行车车棚,一边利用教学楼的后墙(可利用的墙长为19m),另外三边利用学校现有总长38m的铁栏围成。
(1)若围成的面积为180m2,试求出自行车车棚的长和宽;
(2)能围成的面积为200m2自行车车棚吗?如果能,请你给出设计方案;如果不能,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC(∠ACB=90°)的直角边与正方形DEFG的边长均为2,且AC与DE在同一直线上,开始时点C与点D重合,让△ABC沿这条直线向右平移,直到点A与点E重合为止.设CD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )

A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com