
【题目】如图,已知二次函数y=a(x﹣h)2+![]() 的图象经过原点O(0,0),A(2,0).
的图象经过原点O(0,0),A(2,0).
写出该函数图象的对称轴;

【答案】对称轴为直线x=1
【解析】试题分析:
本题要求二次函数的对称轴. 分析题目条件可知本题可以用两种方法解决. 其一,因为已知的两个点均为二次函数与x轴的交点,所以点O与点A必定关于二次函数的对称轴对称. 根据对称性可知,该二次函数的对称轴与x轴的交点必定是线段OA的中点. 利用该几何性质容易得到该二次函数的对称轴. 其二,由于点O与点A均在二次函数的图象上,所以点O与点A的坐标一定满足该二次函数的解析式. 将这两点的坐标代入解析式并联立,即可得到一个方程组,解之可得a与h的值. 这样就确定了该二次函数的解析式,进而可以获得二次函数的对称轴.
试题解析:
(解法一)
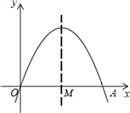
如图,设该二次函数的对称轴与x轴的交点为M.
∵点O与点A均为该二次函数与x轴的交点,
∴点O与点A关于该二次函数的对称轴对称,
∴在x轴上,线段OA的中点为点M,即![]() ,
,
∵点O的坐标为(0, 0),点A的坐标为(2, 0),
∴OA=2,
∴![]() ,
,
∴点M的坐标为(1, 0),
∵点M为该二次函数的对称轴与x轴的交点,
∴该二次函数的对称轴为直线x=1.
(解法二)
∵二次函数![]() 的图象经过点O(0, 0)与点A(2, 0),
的图象经过点O(0, 0)与点A(2, 0),
∴将点O与点A的坐标代入二次函数解析式,得
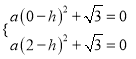 ,
,
解这个方程组:
 ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,①
,①
∵在二次函数![]() 中,a≠0,
中,a≠0,
∴①式两侧同时除以a,得 h=1.
∴![]() .
.
∴该二次函数的解析式为![]() .
.
∴该二次函数的对称轴为直线x=1.


科目:初中数学 来源: 题型:
【题目】一家商店将某种服装按成本价提高40%后标价,又以8折优惠卖出,结果每件作服装仍可获利15元,则这种服装每件的成本是( )
A.120元
B.125元
C.135元
D.140元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师在黑板上写了一个等式:(a+3)x=4(a+3).王聪说x=4,刘敏说不一定,当x≠4时,这个等式也可能成立.你同意谁的观点?请用等式的基本性质说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司对一批某品牌衬衣的质量抽检结果如下表.

(1)从这批衬衣众人抽1件是次品的概率约为多少?
(2)如果销售这批衬衣600件,那么至少要再准备多少件正品衬衣供买到次品的顾客更换?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)有一种可食用的野生菌,刚上市时,外商李经理以每千克30元的市场价格收购了这种野生菌1000千克存放入冷库中,据预测,该野生菌的市场价格将每天每千克上涨1元;但冷冻存放这批野生菌时每天需要支出各种费用合计310元,而且这种野生菌在冷库中最多保存140天,同时,平均每天有3千克的野生菌损坏导致不能出售.
(1)若存放![]() 天后,将这批野生菌一次性出售,设这批野生菌的销售总额为
天后,将这批野生菌一次性出售,设这批野生菌的销售总额为![]() 元,试求出
元,试求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)李经理将这批野生菌存放多少天后一次性全部出售可以获得22500元的利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
(1)求抛物线的解析式;
(2)求出对称轴和顶点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算6+(-3.5)+(+2.5)时,较好的方法是( )
A. 按顺序进行计算B. 同号的数先相加
C. 后面的两个数先相加D. 以上的方法都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张矩形纸片ABCD中,AD=4cm,点E,F分别是CD和AB的中点,现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH,若HG延长线恰好经过点D,则CD的长为_________.
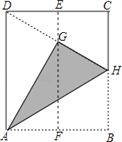
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com