
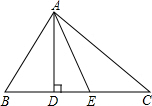
 在△ABC中,AD⊥BC,AE平分∠BAC,∠B=80°,∠C=46°.
在△ABC中,AD⊥BC,AE平分∠BAC,∠B=80°,∠C=46°.分析 (1)先根据三角形内角和定理求出∠BAC的度数,再根据AE平分∠BAC求出∠BAE的度数,根据AD⊥BC求出∠BAD的度数,由∠DAE=∠BAE-∠BAD即可得出结论;
(2)设∠C=α°,∠B=β°,α>β,同(1)即可得出结论.
解答 解:(1)∵在△ABC中,∠B=80°,∠C=46°,
∴∠BAC=180°-80°-46°=54°.
∵AE平分∠BAC,
∴∠BAE=$\frac{1}{2}$∠BAC=27°.
∵AD⊥BC,
∴∠BAD=90°-∠B=90°-80°=10°,
∴∠DAE=∠BAE-∠BAD=27°-10°=17°;
(2)∠DAE=$\frac{1}{2}$(∠B+∠C),理由如下:
∵AD是△ABC的高,
∴∠ADC=90°,
∵∠C=β,
∴∠DAC=90°-β,
∵∠B=α,∠C=β,
∴∠BAC=180°-∠B-∠C=180°-α-β,
∵AE是△ABC的角平分线,
∴∠EAC=$\frac{1}{2}$∠BAC=$\frac{1}{2}$(180°-α-β)=90°-$\frac{1}{2}$α-$\frac{1}{2}$β,
∵∠C>∠B
∴当α>β时,∠DAE=∠DAC-∠EAC=90°-β-(90°-$\frac{1}{2}$α-$\frac{1}{2}$β)=$\frac{1}{2}$α-β=$\frac{1}{2}$(α-β).
点评 本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.


科目:初中数学 来源: 题型:选择题
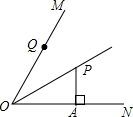 如图,∠MON=60°,OP平分∠MON,PA⊥ON于点A,点Q是射线OM的一个动点,若OP=4,则PQ的最小值为( )
如图,∠MON=60°,OP平分∠MON,PA⊥ON于点A,点Q是射线OM的一个动点,若OP=4,则PQ的最小值为( )| A. | $2\sqrt{3}$ | B. | 4 | C. | 2 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
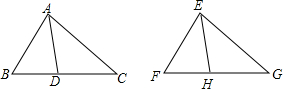 如图,已知△ABC和△EFG中,∠BAC=∠FEC,∠B=∠F,AD、EH分别是∠BAC、∠FEC的平分线,且AD=EH.求证:△ABC≌△EFG.
如图,已知△ABC和△EFG中,∠BAC=∠FEC,∠B=∠F,AD、EH分别是∠BAC、∠FEC的平分线,且AD=EH.求证:△ABC≌△EFG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
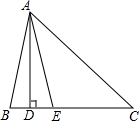 如图,△ABC中,AD⊥BC,AE平分∠BAC.
如图,△ABC中,AD⊥BC,AE平分∠BAC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在靠墙(墙长为20m)的地方围建一个矩形的养鸡场,另三边用竹篱笆围成.如果竹篱笆总长为18m,鸡场的宽(m)与长(m)的函数解析式为y=$9-\frac{x}{2}$,如果宽为2m.那么长为14.
如图,在靠墙(墙长为20m)的地方围建一个矩形的养鸡场,另三边用竹篱笆围成.如果竹篱笆总长为18m,鸡场的宽(m)与长(m)的函数解析式为y=$9-\frac{x}{2}$,如果宽为2m.那么长为14.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com