
分析 (1)设甲、乙两地之间的距离为xkm,根据题意列出方程3(x-510)=x-170,即可解答;
(2)设客车原来的速度为ykm/h,根据题意得:$\frac{680}{y}-\frac{680}{y+6}=3$,解方程即可.
解答 解:(1)设甲、乙两地之间的距离为xkm,根据题意得:
3(x-510)=x-170,
解得:x=680,
答:甲、乙两地之间的距离为680km;
(2)设客车原来的速度为ykm/h,
根据题意得:$\frac{680}{y}-\frac{680}{y+6}=3$,
解得:y1=34,y2=-40(舍去),
经检验知,y=34是原方程的解,
答:客车原来的速度为34km/h.
点评 本题考查了分式方程的应用,解决本题的关键是读懂题意,找出等量关系列方程.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 6 | B. | 9 | C. | 12 | D. | 18 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
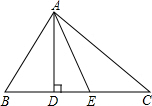 在△ABC中,AD⊥BC,AE平分∠BAC,∠B=80°,∠C=46°.
在△ABC中,AD⊥BC,AE平分∠BAC,∠B=80°,∠C=46°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 20% | B. | 30% | C. | 40% | D. | 50% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com