
分析 (1)根据两卡收费标准分别列式整理即可得解;
(2)把y=200,x=300代入函数关系式进行计算即可得解;根据所缴话费相等列出方程求解即可.
解答 解:(1)A卡:y=0.6x,
B卡:y=0.4x+50;
(2)y=200时,
A:200=0.6x,x=333$\frac{1}{3}$,
B:200=0.4x+50,x=375,
答:A类卡收费标准可以通话333$\frac{1}{3}$分钟,B类卡收费标准可以通话375分钟;
x=300时,
A:y=0.6×300=180元,
B:y=0.4×300+50=170元,
∵180>170,
∴应该选择B卡收费标准;
由题意得,0.4x+500=0.6x,
解得x=250.
答:每月通话250分钟,按A、B两类收费标准缴费,所缴话费相等.
点评 本题考查了一次函数的应用,主要利用了已知自变量求函数值,读懂题目信息,理解两类收费方法的话费组成是解题的关键.


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
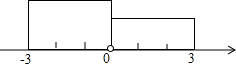 先阅读下列材料,然后再解答问题:
先阅读下列材料,然后再解答问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在靠墙(墙长为20m)的地方围建一个矩形的养鸡场,另三边用竹篱笆围成.如果竹篱笆总长为18m,鸡场的宽(m)与长(m)的函数解析式为y=$9-\frac{x}{2}$,如果宽为2m.那么长为14.
如图,在靠墙(墙长为20m)的地方围建一个矩形的养鸡场,另三边用竹篱笆围成.如果竹篱笆总长为18m,鸡场的宽(m)与长(m)的函数解析式为y=$9-\frac{x}{2}$,如果宽为2m.那么长为14.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
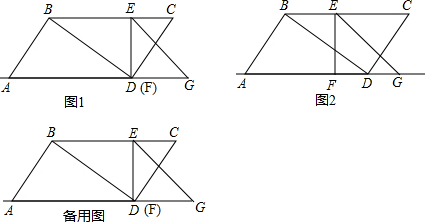
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
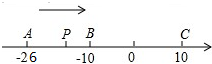 已知数轴上有A、B、C三点,分别表示有理数-26,-10,10,动点P从
已知数轴上有A、B、C三点,分别表示有理数-26,-10,10,动点P从查看答案和解析>>
科目:初中数学 来源: 题型:解答题
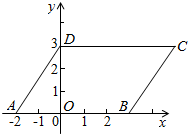 如图,四边形ABCD为平行四边形,OD=3,CD=AB=5,点A坐标为(-2,0)
如图,四边形ABCD为平行四边形,OD=3,CD=AB=5,点A坐标为(-2,0)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com