
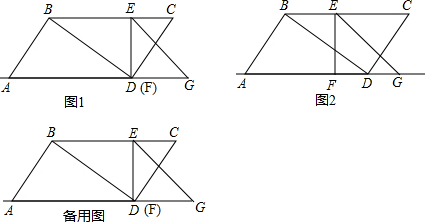
���� ��1�����ȹ���B��BH��AD����AD���H��Ȼ����ֱ��������ABH�У����ݹ��ɶ������AH=3���ٸ���AB2=AH•AD�����AD�ij��Ƕ��ټ��ɣ�
��2������t��ȡֵ��Χ����4������������ۣ������EFG���ABD��ص����ֵ����s���˶�ʱ��t�ĺ�����ϵʽ���Լ�t��ȡֵ��Χ�Ƕ��ټ��ɣ�
��3���������⣬�������������DQ=PQʱ���ڵ�DP=DQʱ���۵�DP=PQʱ���������ۣ��ٸ��ݵ��������ε����ʣ��������ʱ��t��ֵ�Ƕ��٣�
��� �⣺��1����ͼ1������B��BH��AD����AD���H��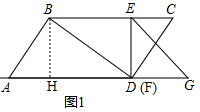 ��
��
��BH��AD��
��AH=$\sqrt{{AB}^{2}{-BH}^{2}}$
=$\sqrt{{5}^{2}{-4}^{2}}$
=3
��BD��AB��
��AB2=AH•AD��
��AD=AB2��AH
=52��3
=$\frac{25}{3}$
��2������ͼ2��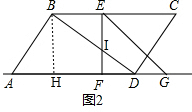 ��
��
��G���D�غϣ���Ҫ��ʱ���ǣ�4��1=4���룩��
��0��t��4ʱ��
DH=AD-AH=$\frac{25}{3}-3=\frac{16}{3}$��DF=t��
��$\frac{FI}{BH}=\frac{DF}{DH}$��
��$\frac{FI}{4}=\frac{t}{\frac{16}{3}}$��
���FI=$\frac{3}{4}t$��
��s=$\frac{1}{2}��DF��FI$
=$\frac{1}{2}t��\frac{3}{4}t$
=${\frac{3}{8}t}^{2}$
����ͼ3��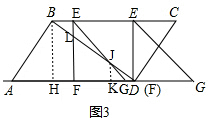 ��
��
��F���H�غϣ���Ҫ��ʱ���ǣ�$\frac{16}{3}$��1=$\frac{16}{3}$���룩��
��4��t��$\frac{16}{3}$ʱ��
��$\frac{LF}{BH}=\frac{DF}{DH}$��
��$\frac{LF}{4}=\frac{t}{\frac{16}{3}}$��
���LF=$\frac{3}{4}$t��
�ߡ�EGF=45�㣬
��JK=KG��
��$\frac{JK}{LF}=\frac{DK}{DF}$��
��$\frac{JK}{\frac{3}{4}t}=\frac{JK+t-4}{t}$��
���JK=3t-12��FK=4-��3t-12��=16-3t��
��s=$\frac{1}{2}����3t-12������3t-12��+$��3t-12$+\frac{3}{4}t$������16-3t����2
=${\frac{9}{2}t}^{2}-36t+72$$+��-{\frac{45}{8}t}^{2}+48t-96��$
=-${\frac{9}{8}t}^{2}+12t$-24
����ͼ4��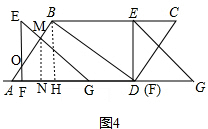 ��
��
��F���A�غϣ���Ҫ��ʱ���ǣ�$\frac{25}{3}$��1=$\frac{25}{3}$���룩��
��$\frac{16}{3}$��t��$\frac{25}{3}$ʱ��
��$\frac{OF}{BH}=\frac{AF}{AH}$��
��$\frac{OF}{4}=\frac{\frac{25}{3}-t}{3}$��
���OF=$\frac{100-12t}{9}$��
��$\frac{MN}{BH}=\frac{AN}{AH}$��
��$\frac{MN}{AN}=\frac{BH}{AH}=\frac{4}{3}$��
��AG=AD-DG=$\frac{25}{3}-��t-4��$=$\frac{37}{3}$-t��AG=AN$+NG=\frac{3}{4}MN+MN$��
��$\frac{3}{4}MN+MN=\frac{37}{3}-t$��
���MN=$\frac{148-12t}{21}$��
��s=$\frac{1}{2}��$��$\frac{37}{3}$-t����$\frac{148-12t}{21}$-$\frac{1}{2}��$��$\frac{25}{3}-t$����$\frac{100-12t}{9}$
=${\frac{2}{7}t}^{2}$$-\frac{148}{21}t$$+\frac{2738}{63}$-${\frac{2}{3}t}^{2}$$+\frac{100}{9}t$$-\frac{1250}{27}$
=-${\frac{8}{21}t}^{2}+\frac{256}{63}t-\frac{536}{189}$
����ͼ5��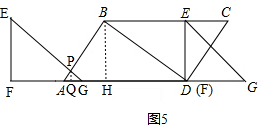 ��
��
��G���A�غϣ���Ҫ��ʱ���ǣ���$\frac{25}{3}$+4����1=$\frac{37}{3}$���룩��
��$\frac{25}{3}$��t��$\frac{37}{3}$ʱ��
AG=AD-DG=$\frac{25}{3}$-��t-4��=$\frac{37}{3}-t$��
��$\frac{AQ}{AH}=\frac{PQ}{BH}$��
��$\frac{AG-PQ}{AH}=\frac{PQ}{BH}$��
��$\frac{\frac{37}{3}-t-PQ}{3}=\frac{PQ}{4}$��
���PQ=$\frac{148-12t}{21}$��
��s=$\frac{1}{2}AG��PQ$
=$\frac{1}{2}����\frac{37}{3}-t����\frac{148-12t}{21}$
=${\frac{2}{7}t}^{2}$$-\frac{148}{21}t$$+\frac{2738}{63}$
���ϣ��ɵ�s��t�ĺ�����ϵʽ�ǣ�
s=$\left\{\begin{array}{l}{{\frac{3}{8}t}^{2}����0��t��4��}\\{-{\frac{9}{8}t}^{2}+12t-24����4��t��\frac{16}{3}��}\\{-{\frac{8}{21}t}^{2}+\frac{256}{63}t-\frac{536}{189}����\frac{16}{3}��t��\frac{25}{3}��}\\{{\frac{2}{7}t}^{2}-\frac{148}{21}t+\frac{2738}{63}����\frac{25}{3}��t��\frac{37}{3}��}\end{array}\right.$
��3������ͼ6��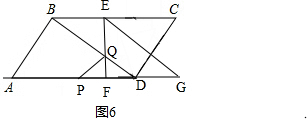 ��
��
��DQ=PQʱ��
��QF��PD��
��PF=DF=t��
��AP=3t��
��3t+t+t=$\frac{25}{3}$��
���t=$\frac{5}{3}$
����ͼ7��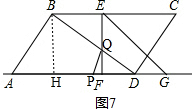 ��
��
��DP=DQʱ��
DP=$\frac{25}{3}-3t$��DF=t��
��$\frac{DF}{DH}=\frac{FQ}{BH}$��
��$\frac{t}{\frac{16}{3}}=\frac{FQ}{4}$��
���FQ=$\frac{3}{4}t$��
��DQ=$\sqrt{{t}^{2}{+��\frac{3}{4}t��}^{2}}=\frac{5}{4}t$��
��$\frac{25}{3}-3t=\frac{5}{4}t$��
���t=$\frac{100}{51}$
����ͼ8��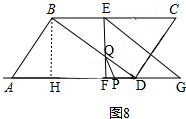 ��
��
��DP=PQʱ��
FP=3t+t-$\frac{25}{3}$=4t-$\frac{25}{3}$��
��$\frac{FQ}{BH}=\frac{DF}{DH}$��
��$\frac{FQ}{4}=\frac{t}{\frac{16}{3}}$��
���FQ=$\frac{3}{4}t$��
��FQ2+FP2=PQ2=DP2��
��${��\frac{3}{4}t��}^{2}{+��4t-\frac{25}{3}��}^{2}{=[t-��4t-\frac{25}{3}��]}^{2}$��
�������ɵ�363t2-800t=0��
���t=$\frac{800}{363}$��t=0����ȥ��
���ϣ��ɵ�
��t=$\frac{5}{3}��\frac{100}{51}��\frac{800}{363}$ʱ����DPQ�ǵ��������Σ�
���� ��1��������Ҫ�����˼��α任�ۺ��⣬�����˺�������ʽ���������˷��������������ռ�����������Ӧ�ã������˷�������˼���Ӧ�ã�Ҫ�������գ�
��2����������������ε���������Լ�ֱ�������ε����ʵ�Ӧ�ã�Ҫ�������գ�
��3���������������������һ��Ҫϸ�ģ�ע���飬���в����������׳�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
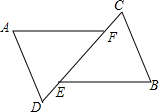 ��ͼ��ʾ����ADF�͡�BCE�У�BE��AF����D��E��F��C��ͬ-ֱ���ϣ�������������ϵʽ����AD=BC����DE=CF���ۡ�A=��B��
��ͼ��ʾ����ADF�͡�BCE�У�BE��AF����D��E��F��C��ͬ-ֱ���ϣ�������������ϵʽ����AD=BC����DE=CF���ۡ�A=��B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
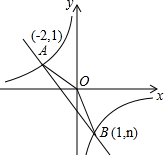 ��ͼ��һ�κ���y=kx+b��ͼ���뷴��������$y=\frac{m}{x}$ͼ���ཻ��A��B���㣬
��ͼ��һ�κ���y=kx+b��ͼ���뷴��������$y=\frac{m}{x}$ͼ���ཻ��A��B���㣬�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com