
分析 首先设40座客车租了x辆,根据租用50座客车,则能少租1辆,且保证前几辆坐满的情况下,最后一辆车还剩下不到20个空座,列出不等式组50-20<40x-50(x-2)<50进行求解;再根据总费用=每辆车费用×车数,可分别求出两种车的总费用,然后进行比较可得出结论.
解答 解:设40座客车租了x辆,则:
50-20<40x-50(x-2)<50,
即:30<100-10x<50,
解得5<x<7,
又因为x是整数,所以x=6,
①租用40座客车的费用为:6×150=900元,
②租用50座客车的费用为:5×170=850元,
又∵900>850,
∴应租用50座客车较为合算.
点评 此题考查了一元一次不等式组的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出不等式组,注意x只能取整数.


科目:初中数学 来源: 题型:解答题
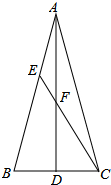
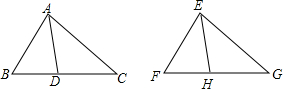 如图,已知△ABC和△EFG中,∠BAC=∠FEC,∠B=∠F,AD、EH分别是∠BAC、∠FEC的平分线,且AD=EH.求证:△ABC≌△EFG.
如图,已知△ABC和△EFG中,∠BAC=∠FEC,∠B=∠F,AD、EH分别是∠BAC、∠FEC的平分线,且AD=EH.求证:△ABC≌△EFG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
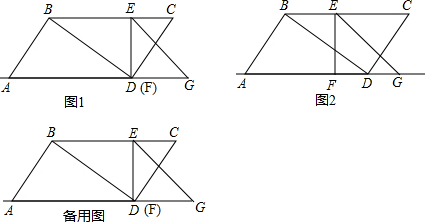
 先阅读下列材料,然后再解答问题:
先阅读下列材料,然后再解答问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
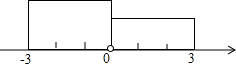
 如图,在靠墙(墙长为20m)的地方围建一个矩形的养鸡场,另三边用竹篱笆围成.如果竹篱笆总长为18m,鸡场的宽(m)与长(m)的函数解析式为y=$9-\frac{x}{2}$,如果宽为2m.那么长为14.
如图,在靠墙(墙长为20m)的地方围建一个矩形的养鸡场,另三边用竹篱笆围成.如果竹篱笆总长为18m,鸡场的宽(m)与长(m)的函数解析式为y=$9-\frac{x}{2}$,如果宽为2m.那么长为14.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
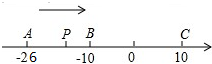 已知数轴上有A、B、C三点,分别表示有理数-26,-10,10,动点P从
已知数轴上有A、B、C三点,分别表示有理数-26,-10,10,动点P从查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}-1$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 1 | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com