
| A. | $\sqrt{3}-1$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 1 | D. | $\frac{{\sqrt{2}}}{2}$ |
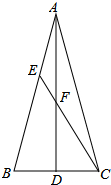
分析 过F点作FG∥BC.根据等腰三角形的性质和三角形内角和定理可得AF=CF,在Rt△CDF中,根据三角函数可得AF=CF=2,DF=$\sqrt{3}$,根据平行线分线段成比例可得比例式GF:BD=AF:AD,求得GF=4-2$\sqrt{3}$,再根据平行线分线段成比例可得比例式EF:EC=GF:BC,依此即可得到EF=$\sqrt{3}$-1.
解答 解:过F点作FG∥BC.
∵在△ABC中,AB=AC,AD是BC边上的中线,
∴BD=CD=$\frac{1}{2}$BC=1,∠BAD=∠CAD=$\frac{1}{2}$∠BAC=15°,AD⊥BC,
∵∠ACE=$\frac{1}{2}$∠BAC,
∴∠CAD=∠ACE=15°,
∴AF=CF,
∵∠ACD=(180°-30°)÷2=75°,
∴∠DCE=75°-15°=60°,
在Rt△CDF中,AF=CF=$\frac{DC}{cos60°}$=2,DF=CD•tan60°=$\sqrt{3}$,
∵FG∥BC,
∴GF:BD=AF:AD,即GF:1=2:(2+$\sqrt{3}$),
解得GF=4-2$\sqrt{3}$,
∴EF:EC=GF:BC,即EF:(EF+2)=(4-2$\sqrt{3}$):2,
解得EF=$\sqrt{3}$-1.
故选:A.
点评 综合考查了等腰三角形的性质,三角形内角和定理可得,三角函数,平行线分线段成比例,以及方程思想,本题的难点是作出辅助线,寻找解题的途径.


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
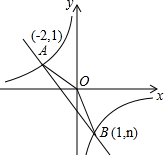 如图,一次函数y=kx+b的图象与反比例函数$y=\frac{m}{x}$图象相交于A、B两点,
如图,一次函数y=kx+b的图象与反比例函数$y=\frac{m}{x}$图象相交于A、B两点,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
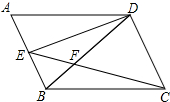 如图,已知四边形ABCD中,AD∥BC,∠A=∠BCD=∠ABD,DE平分∠ADB,下列说法:①AB∥CD;②ED⊥CD;③∠DFC=∠ADC-∠DCE;④S△EDF=S△BCF,其中正确的结论是( )
如图,已知四边形ABCD中,AD∥BC,∠A=∠BCD=∠ABD,DE平分∠ADB,下列说法:①AB∥CD;②ED⊥CD;③∠DFC=∠ADC-∠DCE;④S△EDF=S△BCF,其中正确的结论是( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
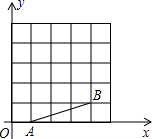 如图,在平面直角坐标系中,A,B,C均在边长为1的正方形网格格点上,反比例函数y=$\frac{k}{x}$(x>0)经过B,C两点.
如图,在平面直角坐标系中,A,B,C均在边长为1的正方形网格格点上,反比例函数y=$\frac{k}{x}$(x>0)经过B,C两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com