
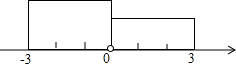
 先阅读下列材料,然后再解答问题:
先阅读下列材料,然后再解答问题:分析 (1)根据题中的解题方法得-3<2x-1<3,然后解不等式组即可;
(2)讨论:当2x-1≥0时,即x≥$\frac{1}{2}$,x+2x-1>3;当2x-1<0时,即x<$\frac{1}{2}$,x-2x+1>3,然后分别解两个不等式组即可得到原不等式的解集;
(3)通过去绝对值,可分类讨论:当x≤0,则-x-2x+1<3;当0<x≤$\frac{1}{2}$时,则x-2x+1<3;当x>$\frac{1}{2}$时,x+2x-1<3,从而可把原不等式化为三个不等式组.
解答 解:(1)-3<2x-1<3,
解得-1<x<2;
(2)当2x-1≥0时,即x≥$\frac{1}{2}$,x+2x-1>3,解得x>$\frac{4}{3}$,所以x>$\frac{4}{3}$,
当2x-1<0时,即x<$\frac{1}{2}$,x-2x+1>3,解得x<-2,所以x<-2,
所以不等式的解集为x>$\frac{4}{3}$或x<-2;
(3)当x≤0,则-x-2x+1<3,
当0<x≤$\frac{1}{2}$时,则x-2x+1<3,
当x>$\frac{1}{2}$时,x+2x-1<3,
所以原不等式可化为$\left\{\begin{array}{l}{x≤0}\\{-x-2x+1<3}\end{array}\right.$或$\left\{\begin{array}{l}{0<x≤\frac{1}{2}}\\{x-2x+1<3}\end{array}\right.$或$\left\{\begin{array}{l}{x>\frac{1}{2}}\\{x+2x-1<3}\end{array}\right.$.
点评 本题考查了解一元一次不等式组:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.注意绝对值的意义的运用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com