
如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD.若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为 .


3
 .
.
【考点】矩形的性质;菱形的性质.
【分析】根据矩形的性质和菱形的性质得∠ABE=∠EBD=∠DBC=30°,AB=BO=3,因为四边形BEDF是菱形,所以可求出BE,AE,进而可求出BC的长.
【解答】解:∵四边形ABCD是矩形,四边形BEDF是菱形,
∴∠A=90°,AD=BC,DE=BF,OE=OF,EF⊥BD,∠EBO=FBO,
∴AE=FC.又EF=AE+FC,
∴EF=2AE=2CF,又EF=2OE=2OF,AE=OE,
∴△ABE≌OBE,
∴∠ABE=∠OBE,
∴∠ABE=∠EBD=∠DBC=30°,
∴BE=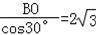
 ,
,
∴BF=BE=2
 ,
,
∴CF=AE=
 ,
,
∴BC=BF+CF=3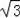
 ,
,
故答案为:3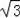
 .
.
【点评】本题考查了矩形的性质、菱形的性质以及在直角三角形中30°角所对的直角边时斜边的一半,解题的关键是求出∠ABE=∠EBD=∠DBC=30°.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
已知某厂现有A种金属70吨,B种金属52吨,现计划用这两种金属生产M、N两种型号的合金产品共80000套,已知做一套M型号的合金产品需要A种金属0.6kg,B种金属0.9kg,可获利润45元;做一套N型号的合金产品需要A种金属1.1kg,B种金属0.4kg,可获利润50元.若设生产N种型号的合金产品套数为x,用这批金属生产这两种型号的合金产品所获总利润为y元.
(1)求y与x的函数关系式,并求出自变量x的取值范围;
(2)在生产这批合金产品时,N型号的合金产品应生产多少套,该厂所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
在矩形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )


A.2和3 B.3和2 C.4和1 D.1和4
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在第1个△A1BC中,∠B=20°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第5个三角形中以A5为顶点的内角度数是 .
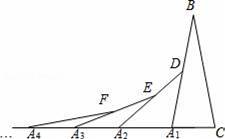

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com