
��֪ij������A�ֽ���70�֣�B�ֽ���52�֣��ּƻ��������ֽ�������M��N�����ͺŵĺϽ��Ʒ��80000�ף���֪��һ��M�ͺŵĺϽ��Ʒ��ҪA�ֽ���0.6kg��B�ֽ���0.9kg���ɻ�����45Ԫ����һ��N�ͺŵĺϽ��Ʒ��ҪA�ֽ���1.1kg��B�ֽ���0.4kg���ɻ�����50Ԫ����������N���ͺŵĺϽ��Ʒ����Ϊx�����������������������ͺŵĺϽ��Ʒ����������ΪyԪ��
��1����y��x�ĺ�����ϵʽ��������Ա���x��ȡֵ��Χ��
��2�������������Ͻ��Ʒʱ��N�ͺŵĺϽ��ƷӦ���������ף��ó��������������������Ƕ��٣�
�����㡿һ�κ�����Ӧ�ã�
��ר�⡿Ӧ���⣮
����������1���������������M��N�����ͺźϽ��Ʒ������֮����ʽ�������ɣ��ٸ���M��N���ֺϽ�����A��B���ֽ������������н����г�����ʽ����⼴�ɣ�
��2������һ�κ�������������������������ֵ���ɣ�
����𡿽⣺��1��y=50x+45��80000��x��=5x+3600000��
������ã�
 ��
��
�ⲻ��ʽ�ٵã�x��44000��
�ⲻ��ʽ�ڵã�x��40000��
���ԣ�����ʽ��Ľ⼯��40000��x��44000��
��y��x�ĺ�����ϵʽ��y=5x+3600000��40000��x��44000����
��2����k=5��0��
��y��x�����������
�൱x=44000ʱ��y���=3820000��
������N�ͺŵĺϽ��Ʒ44000��ʱ���ó���������������������3820000Ԫ��
�����������⿼����һ�κ�����Ӧ�ã�һԪһ�β���ʽ���Ӧ�ã�����һ�κ�������ֵʱ���ؼ���Ӧ��һ�κ��������ʣ����ɺ���y��x�ı仯������Ա�����ȡֵ��Χȷ����ֵ��


 �ŵ������ϵ�д�
�ŵ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪�߳�Ϊ3��������ABCD�У���E������BC�ϣ���BE��2CE������AE������DC�ڵ�F������ABE��ֱ��AE���ۣ���B���ڵ�B1����
��1����ͼ1������E���߶�BC�ϣ���CF�ij���
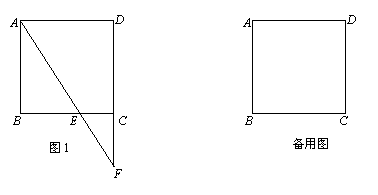 ��2����sin��DAB1��ֵ.
��2����sin��DAB1��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����ֱ��y=��2x��y������ƽ��3����λ���ȣ�����ֱ�ߵĺ�����ϵʽΪ��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ������ij�в��ּ�ͼ����֪ҽԺ������Ϊ����2����2�����뽨��ƽ��ֱ������ϵ���ֱ�д��������ص����꣮


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ���ھ���ABCD�У���AB�ij�Ϊ3����E��F�ֱ���AD��BC�ϣ�����BE��DF��EF��BD�����ı���BEDF�����Σ���EF=AE+FC�����BC�ij�Ϊ��������������


�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com