
分析 (1)分组使用平方差公式,再利用自然数求和公式解题;
(2)由已知得,12=1,12-22=-3,12-22+32=6,12-22+33-42=-10,根据已知可得等式的左边是正整数的平方和,当n为奇数时,符号为正;当n为偶数时,符号为负;所以归纳推理可知,第n个式子.
解答 解:(1)原式=(12-22)+(32-42)+…+(992-1002)
=(1-2)(1+2)+(3-4)(3+4)+…+(99-100)(99+100)
=-(1+2)-(3+4)-…-(99+100)
=-(1+2+3+4+…+99+100)
=-5050;
(2)由已知得,12=1=(-1)2×$\frac{1×(1+1)}{2}$,
12-22=-3=(-1)3×$\frac{2×(2+1)}{2}$,
12-22+32=6=(-1)4×$\frac{3×(3+1)}{2}$,
12-22+33-42=-10=(-1)5×$\frac{4×(4+1)}{2}$,
…
根据已知可得等式的左边是正整数的平方和,当n为奇数时,符号为正,当n为偶数时,符号为负,
所以归纳推理可知,第n个式子为12-22+32-42+…+(-1)n+1n2=(-1)n+1$\frac{n(n+1)}{2}$.
点评 本题考查了平方差公式的运用,归纳推理,根据已知归纳推理出规律是解答此题的关键.


科目:初中数学 来源: 题型:选择题
| A. | -2.14既是负数、分数,也是有理数 | |
| B. | 0既不是正数也不是负数,但是整数 | |
| C. | 0是非正数 | |
| D. | -2012既是负数,也是整数,但不是有理数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 年龄组 | 13岁 | 14岁 | 15岁 | 16岁 |
| 参赛人数 | 9 | 15 | 3 | 3 |
| A. | 14.5,14.5 | B. | 14,15 | C. | 14.5,14 | D. | 14,14 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
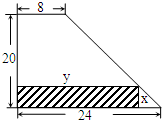 某厂有许多形状为直角梯形的铁皮边角料,如图,为降低消耗,现要从这些边角料上截取矩形铁片(图中阴影部分)备用,当截取的矩形面积最大时,矩形的两边长x、y应为( )
某厂有许多形状为直角梯形的铁皮边角料,如图,为降低消耗,现要从这些边角料上截取矩形铁片(图中阴影部分)备用,当截取的矩形面积最大时,矩形的两边长x、y应为( )| A. | x=15,y=12 | B. | x=12,y=15 | C. | x=14,y=10 | D. | x=10,y=14 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
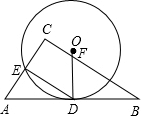 如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC交于点E,且DE∥BC,连接OD,与BC相交于点F
如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC交于点E,且DE∥BC,连接OD,与BC相交于点F查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com