
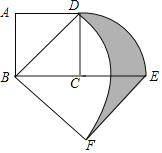
【题目】如图,正方形ABCD中,AB=2,将线段CD绕点C顺时针旋转90°得到线段CE,线段BD绕点B顺时针旋转90°得到线段BF,连接EF,则图中阴影部分的面积是_______.
【答案】![]() .
.
【解析】
分别求出DC=BC=CE=2,BD=BF=2![]() ,求出∠DCE=90°,∠DBF,分别求出△BCD、△BEF、扇形DBF、扇形DCE的面积,即可得出答案.
,求出∠DCE=90°,∠DBF,分别求出△BCD、△BEF、扇形DBF、扇形DCE的面积,即可得出答案.
过F作FM⊥BE于M,则∠FME=∠FMB=90°,
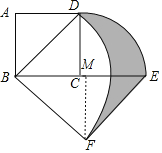
∵四边形ABCD是正方形,AB=2,
∴∠DCB=90°,DC=BC=AB=2,∠DCB=45°,
由勾股定理得:BD=2![]() ,
,
∵将线段CD绕点C顺时针旋转90°得到线段CE,线段BD绕点B顺时针旋转90°得到线段BF,
∴∠DCE=90°,BF=BD=2![]() ,∠FBE=90°-45°=45°,
,∠FBE=90°-45°=45°,
∴BM=FM=2,ME=2,
∴阴影部分的面积S=S△BCD+S△BFE+S扇形DCE-S扇形DBF
=![]() ×2×2+
×2×2+![]() ×4×2+
×4×2+![]() -
-![]()
=6-π,
故答案为:6-π.


科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AC,BC是⊙O的两条弦,过点C作∠BCD=∠A,CD交AB的延长线于点D.
(1)试说明:CD是⊙O的切线;
(2)若tanA=![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,若AB=7,DE平分∠ADC交AC于点E,求ED的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行了“防溺水”知识竞赛,八年级两个班选派10名同学参加预赛,依据各参赛选手的成绩(均为整数)绘制了统计表和折线统计图(如图所示).
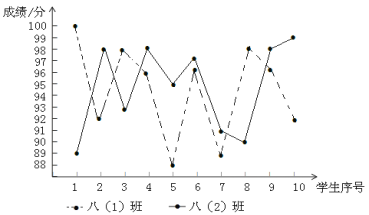
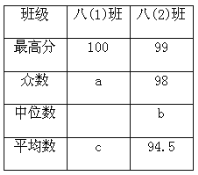
(1)统计表中,a=________, b =________;
(2)若从两个班的预赛选手中选四名学生参加决赛,其中两个班的第一名直接进入决赛,另外两个名额 在成绩为98分的学生中任选两个,求另外两个决赛名额落在不同班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
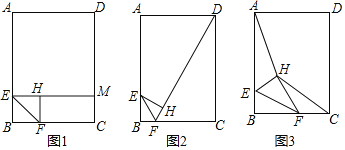
【题目】如图,点E,F分别在矩形ABCD的边AB,BC上,连接EF,将△BEF沿直线EF翻折得到△HEF,AB=8,BC=6,AE:EB=3:1.
(1)如图1,当∠BEF=45°时,EH的延长线交DC于点M,求HM的长;
(2)如图2,当FH的延长线经过点D时,求tan∠FEH的值;
(3)如图3,连接AH,HC,当点F在线段BC上运动时,试探究四边形AHCD的面积是否存在最小值?若存在,求出四边形AHCD的面积的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
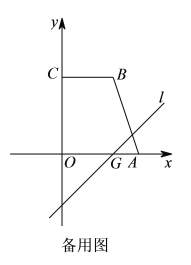
【题目】如图,抛物线y=ax2+bx+6过点A(6,0),B(4,6),与y轴交于点C.
(1)求该抛物线的解析式;
(2)如图1,直线l的解析式为y=x,抛物线的对称轴与线段BC交于点P,过点P作直线l的垂线,垂足为点H,连接OP,求△OPH的面积;
(3)把图1中的直线y=x向下平移4个单位长度得到直线y=x-4,如图2,直线y=x-4与x轴交于点G.点P是四边形ABCO边上的一点,过点P分别作x轴、直线l的垂线,垂足分别为点E,F.是否存在点P,使得以P,E,F为顶点的三角形是等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E |
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |
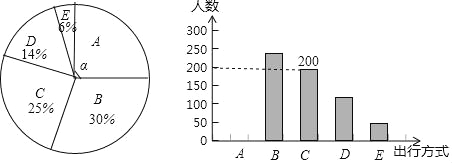
根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有 人,其中选择B类的人数有 人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数![]() ,有下列结论:①其图象与x轴一定相交;②若
,有下列结论:①其图象与x轴一定相交;②若![]() ,函数在
,函数在![]() 时,y随x的增大而减小;③无论a取何值,抛物线的顶点始终在同一条直线上;④无论a取何值,函数图象都经过同一个点.其中所有正确的结论是___.(填写正确结论的序号)
时,y随x的增大而减小;③无论a取何值,抛物线的顶点始终在同一条直线上;④无论a取何值,函数图象都经过同一个点.其中所有正确的结论是___.(填写正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
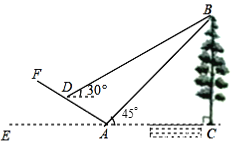
【题目】如图,小明为了测量小河对岸大树BC的高度,他在点A测得大树顶端B的仰角是45°,沿斜坡走![]() 米到达斜坡上点D,在此处测得树顶端点B的仰角为30°,且斜坡AF的坡比为1︰2.则小明从点A走到点D的过程中,他上升的高度为____米;大树BC的高度为____米(结果保留根号).
米到达斜坡上点D,在此处测得树顶端点B的仰角为30°,且斜坡AF的坡比为1︰2.则小明从点A走到点D的过程中,他上升的高度为____米;大树BC的高度为____米(结果保留根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com