
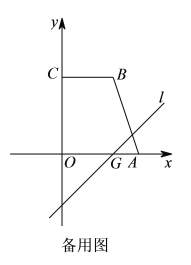
����Ŀ����ͼ��������y=ax2+bx+6����A(6��0)��B(4��6)����y�ύ�ڵ�C��
��1����������ߵĽ���ʽ��
��2����ͼ1��ֱ��l�Ľ���ʽΪy=x�������ߵĶԳ������߶�BC���ڵ�P������P��ֱ��l�Ĵ��ߣ�����Ϊ��H������OP������OPH�������
��3����ͼ1�е�ֱ��y=x����ƽ��4����λ���ȵõ�ֱ��y=x-4����ͼ2��ֱ��y=x-4��x�ύ�ڵ�G����P���ı���ABCO���ϵ�һ�㣬����P�ֱ���x�ᡢֱ��l�Ĵ��ߣ�����ֱ�Ϊ��E��F���Ƿ���ڵ�P��ʹ����P��E��FΪ������������ǵ��������Σ���������ֱ��д����P�����ꣻ�������ڣ���˵��������


���𰸡���1��![]() ��2��S��OPH=8����3���������������ĵ�P����P����Ϊ����0��4��,��
��2��S��OPH=8����3���������������ĵ�P����P����Ϊ����0��4��,��![]() ��
��![]() ��,��4��6��,��
��,��4��6��,��![]() ��6����
��6����
��������
��1����![]() ��
��![]() �������ʽ����⼴�ɣ�
�������ʽ����⼴�ɣ�
��2���ӳ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() ��
��![]() ��Ϊ����ֱ�������Σ�����
��Ϊ����ֱ�������Σ�����![]() ���㼴�ɣ�
���㼴�ɣ�
��3�����ڵ�![]() ������
������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ϣ������������α�����������������ʷֱ���������㼴��.
�ϣ������������α�����������������ʷֱ���������㼴��.
��1����������y=ax2+bx+6����A(6��0)��B(4��6)��
![]()
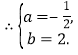 ��
��![]()
��2���߸������ߵĶԳ���Ϊֱ��![]() ��CP=2��
��CP=2��
��ͼ1���ӳ�HP��y���ڵ�M������OMH����CMP��Ϊ����ֱ�������Σ�
��CM=CP=2��
��OM=OC+CM=6+2=8�� OH=MH=![]()
S��OPH=S��OMH��S��OMP=![]()
��3���������������ĵ�P����P����Ϊ��
��0��4��,��![]() ��
��![]() ��,��4��6��,��
��,��4��6��,��![]() ��6����
��6����


 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
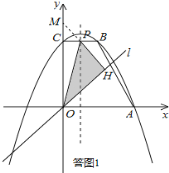
����Ŀ����ͼ������ABC�У���B��40������C��80������Ҫ��������и��⣺
��1������ABC�ĸ�AD��
��2������ABC�Ľ�ƽ����AE��
��3��������������ͼ�����DAE�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
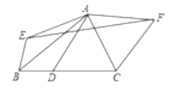
����Ŀ����ͼ���ı���ABCD�������Σ�BE��EF��DF��EF��BE��2.5dm��DF��4dm����ôEF�ij�Ϊ�� ��

A. 6.5dm B. 6dm C. 5.5dm D. 4dm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ԲO��ֱ��ΪAB��D�ǰ�Բ�ϵ�һ�����㣨�����A��B�غϣ�������BD���ӳ�����C��ʹCD=BD������D����ԲO�����߽�AC�ڵ�E��
��1�������DE��AC��λ�ù�ϵ����˵�����ɣ�
��2����AB=6��BD=2ʱ����DE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ABCD��һ����OΪֱ�Ƕ�������ǰ壬�ƶ����ǰ壬ʹ���ǰ����ֱ�DZ�����ֱ�߷ֱ���ֱ��BC��CD���ڵ�M��N��
��ͼ1������O���A�غϣ����õ��߶�OM��ON�Ĺ�ϵ��
��1���۲���룺��ͼ2������O�������ε����ģ��������Խ��ߵĽ��㣩��OM��ON��������ϵ��___________��
��2��̽��֤������ͼ3������O�������ε��ڲ������߽磩����OM=ON�����ж����ǰ��ƶ��������������������ĵ�O�����ʲôͼ�Σ���˵�����ɣ�
��3����չ���죺����O�������ε��ⲿ����OM=ON��������ͼ4�л�������������һ����������������ǰ��ڸ�������£����ⲿ���ƶ����������������ĵ�O����ɵ�ͼ������д����ȷ�Ľ��ۣ�������˵��




�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���ABC��������������ֱ�ΪA��-3��0����B��-3��-4����C��-1��-4����
��1�����ABC�������
��2����ͼ��������ABC����x��ԳƵ�ͼ�Ρ�DEF����A��B��C�ĶԳƵ�ֱ�ΪD��E��F����д��D��E��F�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y1��ax2��bx��c(a��0)�Ķ���������(1��4)������ֱ��y2��x��1��һ������ĺ�����Ϊ2.
(1)�������ߵĽ���ʽ��
(2)�ڸ���������ϵ�л���������y1��ax2��bx��c(a��0)��ֱ��y2��x��1��ͼ������ͼ��ֱ��д��ʹy1��y2��x��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �У���
����![]()
![]() ��
��![]() ��
��![]() �����Ϊ
�����Ϊ![]() ��
��![]() Ϊ
Ϊ![]() ����һ���㣨����
����һ���㣨����![]() ��
��![]() �غϣ�����
�غϣ�����![]() ��
��![]() �ֱ���ֱ��
�ֱ���ֱ��![]() ��
��![]() ���۵õ�
���۵õ�![]() ��
��![]() ����ô��
����ô��![]() ���������СֵΪ____��
���������СֵΪ____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣���ABC�У�AB=AC����B����C��ƽ���߽���O�㣬��O����EF��BC��AB��AC��E��F���Իش�

��1��ͼ�е����������� �����룺EF��BE��CF֮��Ĺ�ϵ�� �����ɣ�
��2����ͼ�ڣ���AB��AC��ͼ�е����������� ���ڵڣ�1������EF��BE��CF��Ĺ�ϵ��������
��3����ͼ�ۣ�����ABC�С�B��ƽ����BO�����������ƽ����CO����O����O����OE��BC��AB��E����AC��F����ʱͼ�л��е�����������EF��BE��CF��ϵ����Σ�˵��������ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com