
【题目】如图,![]() 中,∠
中,∠![]()
![]() ,
,![]() ,
,![]() 的面积为
的面积为![]() ,
,![]() 为
为![]() 边上一动点(不与
边上一动点(不与![]() ,
,![]() 重合),将
重合),将![]() 和
和![]() 分别沿直线
分别沿直线![]() ,
,![]() 翻折得到
翻折得到![]() 和
和![]() ,那么△
,那么△![]() 的面积的最小值为____.
的面积的最小值为____.
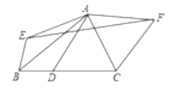
【答案】4.
【解析】
过E作EG⊥AF,交FA的延长线于G,由折叠可得∠EAG=30°,而当AD⊥BC时,AD最短,依据BC=7,△ABC的面积为14,即可得到当AD⊥BC时,AD=4=AE=AF,进而得到△AEF的面积最小值为:![]() AF×EG=
AF×EG=![]() ×4×2=4.
×4×2=4.
解:如图,过E作EG⊥AF,交FA的延长线于G,
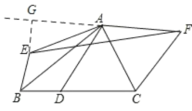
由折叠可得,AF=AE=AD,∠BAE=∠BAD,∠DAC=∠FAC,
∵∠BAC=75°,
∴∠EAF=150°,
∴∠EAG=30°,
∴EG=![]() AE=
AE=![]() AD,
AD,
当AD⊥BC时,AD最短,
∵BC=7,△ABC的面积为14,
∴当AD⊥BC时,
![]() ,
,
即:![]()
![]() ,
,
∴![]() .
.
∴△AEF的面积最小值为:![]() AF×EG=
AF×EG=![]() ×4×2=4,
×4×2=4,
故答案为:4.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】某洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示,根据图象解答下列问题:
(1)在这个变化过程中,自变量、因变量是什么?
(2)洗衣机的进水时间是多少分钟?清洗时洗衣机的水量是多少升?
(3)时间为10分钟时,洗衣机处于哪个过程?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+6过点A(6,0),B(4,6),与y轴交于点C.
(1)求该抛物线的解析式;
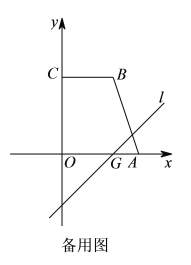
(2)如图1,直线l的解析式为y=x,抛物线的对称轴与线段BC交于点P,过点P作直线l的垂线,垂足为点H,连接OP,求△OPH的面积;
(3)把图1中的直线y=x向下平移4个单位长度得到直线y=x-4,如图2,直线y=x-4与x轴交于点G.点P是四边形ABCO边上的一点,过点P分别作x轴、直线l的垂线,垂足分别为点E,F.是否存在点P,使得以P,E,F为顶点的三角形是等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,若点
,若点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 的速度沿折线
的速度沿折线![]() 运动,设运动时间为
运动,设运动时间为![]() 秒
秒![]() .
.

(1)若点![]() 在
在![]() 上,且满足
上,且满足![]() 时,求出此时
时,求出此时![]() 的值;
的值;
(2)若点![]() 恰好在
恰好在![]() 的角平分线上,求
的角平分线上,求![]() 的值;
的值;
(3)在运动过程中,直接写出当![]() 为何值时,
为何值时,![]() 为等腰三角形.
为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的一条弦,OD⊥AB,垂足为点C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;
(2)若CD=2,AB=8,求半径的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(1,0),(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知四边形ABCD为平行四边形,BE平分∠ABC交AD于点E.
(1)若∠AEB=25°,求∠C的度数;
(2)若AE=5 cm,求CD的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB交弧BC于点D,连结CD、OD,给出以下四个结论:①AC∥OD;②CE=OE;③△ODE∽△ADO;④![]() .其中正确结论的序号是( )
.其中正确结论的序号是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,线段AM为BC边上的高.动点D在射线AM上时,以CD为一边在CD的下方作等边△CDE,连结BE.

(1)填空:∠ACB=______度;
(2)若点D在线段AM上时,求证:△ADC≌△BEC;
(3)当动点D在射线AM上时,设直线BE与直线AM的交点为O,试判断∠AOB是否为定值?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com