
����Ŀ������������ABCD��һ����OΪֱ�Ƕ�������ǰ壬�ƶ����ǰ壬ʹ���ǰ����ֱ�DZ�����ֱ�߷ֱ���ֱ��BC��CD���ڵ�M��N��
��ͼ1������O���A�غϣ����õ��߶�OM��ON�Ĺ�ϵ��
��1���۲���룺��ͼ2������O�������ε����ģ��������Խ��ߵĽ��㣩��OM��ON��������ϵ��___________��
��2��̽��֤������ͼ3������O�������ε��ڲ������߽磩����OM=ON�����ж����ǰ��ƶ��������������������ĵ�O�����ʲôͼ�Σ���˵�����ɣ�
��3����չ���죺����O�������ε��ⲿ����OM=ON��������ͼ4�л�������������һ����������������ǰ��ڸ�������£����ⲿ���ƶ����������������ĵ�O����ɵ�ͼ������д����ȷ�Ľ��ۣ�������˵��




���𰸡���1����ȣ�OM=ON������2���жϣ����ǰ��ƶ��������������������ĵ�O������߶�AC���Խ���AC����֤�������������3�����������
��������
��1������![]() ��
��![]() ����ͨ���ж�
����ͨ���ж�![]() �����Եõ�
�����Եõ�![]() ��
��
��2������![]() ��
��![]() ����
����![]() ������ͨ���ж�
������ͨ���ж�![]() ���ó�
���ó�![]() ���������ֵ�
���������ֵ�![]() ��
��![]() ��ƽ�����ϣ�
��ƽ�����ϣ�
��3����ͼ4���������ã�2�����������ߵķ������ж�������ȫ�Ȳ��ó�����.
��1����ȣ�OM=ON����
��2���жϣ����ǰ��ƶ��������������������ĵ�O������߶�AC���Խ���AC��.
��ͼ3������O�ֱ���OE��BC��OF��CD������ֱ�ΪE��F������OEM=��OFN=90�㣮

���ߡ�C=90�㣬
���EOF=��MON =90��.
���MOE=��NOF��
����MOE����NOF�����ߡ�OEM=��OFN����MOE=��NOF��OM=ON��
���MOE�ա�NOF��AAS��.
��OE=OF��
����OE��BC��OF��CD��
����O����C�Ľ�ƽ������.
�����ǰ��ƶ��������������������ĵ�O������߶�AC���Խ���AC��.
��3����ͼ��ͼ4��
���ǰ��ƶ��������������������ĵ�O�����ֱ��AC�����C����AC��ֱ��ֱ����


 ��������������������ϵ�д�
��������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ֱ�����ABC�ı�AB��AC����ֱ��Ϊ�Գ�������ABC�ĶԳ�ͼ����ABD����ACE����BAC��150�����߶�BD��CE�ཻ�ڵ�O������BE��ED��DC��OA�������½��ۣ��١�EAD��90�����ڡ�BOE��60������OAƽ�֡�BOC����2EA��ED����BP��EQ��������ȷ�Ľ��۸���Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
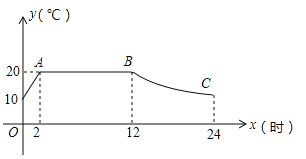
����Ŀ������ij�߲�����������װ�к���ϵͳ�Ĵ�������һ�����������¶�Ϊ15��20�����Ʒ�֣���ͼ��ij�����ϵͳ�ӿ������رռ��رպ������¶�y���棩��ʱ��x��h���仯�ĺ���ͼ������AB���Ǻ��½Σ�BC����˫����![]() ��һ���֣������ͼ����Ϣ����������⣺
��һ���֣������ͼ����Ϣ����������⣺
��1����k��ֵ��
��2������ϵͳ��һ���ڱ��ִ������¶���15�漰15�����ϵ�ʱ���ж���Сʱ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У�AB=AC����D��ֱ��BC��һ�㣨����B��C�غϣ�����ADΪһ����AD���Ҳ�����ADE��ʹAD=AE����DAE =��BAC������CE��
��1����ͼ1������D���߶�BC�ϣ������BAC=90��������BCE=________�ȣ�
��2����![]() ��
��![]() ��
��
����ͼ2���������߶�BC���ƶ�����![]() ��
��![]() ֮����������������ϵ����˵�����ɣ�
֮����������������ϵ����˵�����ɣ�
�ڵ�����ֱ��BC���ƶ�����![]() ��
��![]() ֮����������������ϵ����ֱ��д����Ľ��ۣ�
֮����������������ϵ����ֱ��д����Ľ��ۣ�




�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ƺӣ�����һ��ԴԶ����������׳������Ȼ�ӣ�����һ�������л��������������ĸ�ӣ���ѧ����ʵ����У�С�ֺ�ͬѧ���ڻƺ��ϰ�С·�ϵ�A��B���㴦���ò���Ƿֱ�Ա����Ĺ۾�ͤD���в�������ͼ����á�DAC=45�㣬��DBC=65������AB=200�ף���۾�ͤD��С·AC�ľ���ԼΪ�����ף��������ȷ��1�ף��ο����ݣ�sin65���0.91��cos65���0.42��tan65���2.14��


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
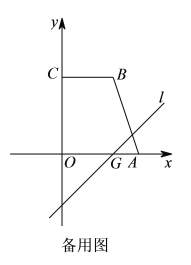
����Ŀ����ͼ��������y=ax2+bx+6����A(6��0)��B(4��6)����y�ύ�ڵ�C��
��1����������ߵĽ���ʽ��
��2����ͼ1��ֱ��l�Ľ���ʽΪy=x�������ߵĶԳ������߶�BC���ڵ�P������P��ֱ��l�Ĵ��ߣ�����Ϊ��H������OP������OPH�������
��3����ͼ1�е�ֱ��y=x����ƽ��4����λ���ȵõ�ֱ��y=x-4����ͼ2��ֱ��y=x-4��x�ύ�ڵ�G����P���ı���ABCO���ϵ�һ�㣬����P�ֱ���x�ᡢֱ��l�Ĵ��ߣ�����ֱ�Ϊ��E��F���Ƿ���ڵ�P��ʹ����P��E��FΪ������������ǵ��������Σ���������ֱ��д����P�����ꣻ�������ڣ���˵��������


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��Ӧ������֯���������̼�������ĺ��٣��������������������������г��ϰ࣮��һ�죬���������г��Ӽ��ﵽ�����ϰ࣬;�������г��������ϣ���������һ��ʱ�䣬���ú�������У�ֱ�����﹤���������������г�������������ʻ����������ҵľ���y���ף������ʱ��x�����ӣ��Ĺ�ϵ��ʾ����ͼ��
��1�������Ӽҳ��������ֹ���ʱ���ٶ�Ϊ �ף����ӣ�
��2����������ʱ ���ӣ�
��3�����߶�OA����Ӧ�ĺ�����ϵʽ����Ҫ��д���Ա�����ȡֵ��Χ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��һ���ң�OD��AB������Ϊ��C������O�ڵ�D����E�ڡ�O�ϣ�
��1������AOD=52�������DEB�Ķ�����
��2����CD=2��AB=8����뾶�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���![]() ��ʵ����
��ʵ����
��1����![]() ȡֵ��Χ��
ȡֵ��Χ��
��2����ԭ���̵�����ʵ����Ϊ![]() ����
����![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com