
【题目】如图,矩形A′B′C′D′在矩形ABCD内部.AB∥A′B′,AD∥A′D′,且AD∶AB=2∶1,设AB与A′B′,BC与B′C′,CD与C′D′,DA与D′A′之间的距离分别为a,b,c,d,要使矩形A′B′C′D′∽矩形ABCD,a,b,c,d满足什么条件?请说明理由.

 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由不同生产商提供![]() 套校服参加比选,甲、乙、两三个同学分别参加比选,比选后结果是:每套校服至少有一人选中,且每人都选中了其中的
套校服参加比选,甲、乙、两三个同学分别参加比选,比选后结果是:每套校服至少有一人选中,且每人都选中了其中的![]() 套校服.如果将其中只有
套校服.如果将其中只有![]() 人选中的校服称作“不受欢迎校服”,
人选中的校服称作“不受欢迎校服”,![]() 人选中的校服称作“颇受欢迎校服”,
人选中的校服称作“颇受欢迎校服”,![]() 人都选中的校服称作“最受欢迎校服”,则“不受欢迎校服”比“最受欢迎校服”多________________套.
人都选中的校服称作“最受欢迎校服”,则“不受欢迎校服”比“最受欢迎校服”多________________套.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6cm,BC=12cm.. 点M从点A开始沿AB边向点B以1cm/秒的速度向B点移动,点N从点B开始沿BC边以2cm/秒的速度向点C移动. 若M, N分别从A, B点同时出发,设移动时间为t (0<t<6),△DMN的面积为S.
(1) 求S关于t的函数关系式,并求出S的最小值;
(2) 当△DMN为直角三角形时,求△DMN的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图所示,已知△ABC和△BDE都是等边三角形,下列结论:①AE=CD;②BF=BG;③BH平分∠AHD;④∠AHC=60°;⑤△BFG是等边三角形;⑥FG∥AD,其中正确的有( )

A. 3个 B. 4个 C. 5个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
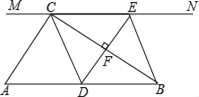
【题目】如图:在Rt△ABC中,∠ACB=90°,AB=6,过点C的直线MN∥AB,D为AB上一点,过点D作DE⊥BC,交直线MN于点E,垂足为F,连结CD,BE,
(1)当点D是AB的中点时,四边形BECD是什么特殊四边形?说明你的理由
(2)在(1)的条件下,当∠A= 时四边形BECD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年6月6日,工信部正式向四家电信企业发放![]() 商用牌照,标志着
商用牌照,标志着![]() 元年开始华为公司作为
元年开始华为公司作为![]() 行业的领军者,已经具备从芯片、产品到系统组网的世界领先的
行业的领军者,已经具备从芯片、产品到系统组网的世界领先的![]() 技术,是全球唯一一家能够提供端到端
技术,是全球唯一一家能够提供端到端![]() 商用解决方案的通讯企业为了了解某中学生对
商用解决方案的通讯企业为了了解某中学生对![]() 通讯技术的了解情况,随机抽取部分学生进行问卷,将结果分成“非常了解”“比较了解”、“一般了解”、“不了解”四种类型,分别记为
通讯技术的了解情况,随机抽取部分学生进行问卷,将结果分成“非常了解”“比较了解”、“一般了解”、“不了解”四种类型,分别记为![]() ,根据调查结果给制了如下尚不完整的两个统计图
,根据调查结果给制了如下尚不完整的两个统计图
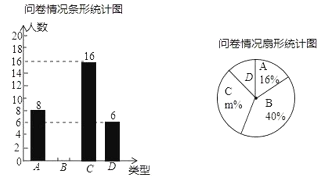
(1)本次问卷共随机调查了 名学生,在扇形统计图中![]() _ _,“
_ _,“![]() ”所在扇形的圆心角的度数为 度;
”所在扇形的圆心角的度数为 度;
(2)请根据数据信息补全条形统计图;
(3)若该校有![]() 名学生,估计选择“非常了解”、“比较了解”的学生共约有多少人?
名学生,估计选择“非常了解”、“比较了解”的学生共约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com