
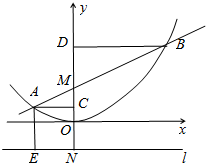
 ��ͼ��ʾ����y����һ��M��0��1����ֱ������κ���y=$\frac{1}{4}$x2��ͼ����A��B���㣬��A��B����ֱ���y��Ĵ��ߣ�����ΪC��D��ֱ��l����M����ԭ��O�ĶԳƵ�N������y�ᴹֱ������A��l�Ĵ��ߣ�����ΪE��
��ͼ��ʾ����y����һ��M��0��1����ֱ������κ���y=$\frac{1}{4}$x2��ͼ����A��B���㣬��A��B����ֱ���y��Ĵ��ߣ�����ΪC��D��ֱ��l����M����ԭ��O�ĶԳƵ�N������y�ᴹֱ������A��l�Ĵ��ߣ�����ΪE������ ��1������A��ĺ�������-1���A�����꣬����M��0��1���ó�AE�ij������ݹ��ɶ������AM�ij��������ɵó����ۣ�
��2����A��xA��yA����B��xB��yB������ֱ��AB�ĺ�������ʽΪy=kx+1�����ɸ���ϵ���Ĺ�ϵ���ɵó����ۣ�
��3����AB���е�ΪP����P��B��ֱ��l�Ĵ��ߣ�����ֱ�ΪQ��F����PQΪ����AEFB����λ�ߣ��ɣ���֪xA•xB=-4��xA+xB=4k����yA=kxA+1��yB=kxB+1�������ε���λ�߶����ó�PQ�ij������ɹ��ɶ������ɵó����ۣ�
���  ����֤������A��ĺ�������-1��
����֤������A��ĺ�������-1��
��A��-1��$\frac{1}{4}$����
�֡�M��0��1����
��AE=$\frac{1}{4}$+1=$\frac{5}{4}$��
��Rt��ACM��
��AM=$\sqrt{{AC}^{2}+{MC}^{2}}$=$\sqrt{{1}^{2}+��1-\frac{1}{4}��^{2}}$=$\sqrt{1+\frac{9}{16}}$=$\frac{5}{4}$��
��AM=AE=$\frac{5}{4}$��
���⣺��A��xA��yA����B��xB��yB������ֱ��AB�ĺ�������ʽΪy=kx+1��
��$\left\{\begin{array}{l}y=\frac{1}{4}{x}^{2}\\ y=kx+1\end{array}\right.$�ɵ�x2-4kx-4=0��
�˷���֮����ΪA��B����ĺ�����xA��xB��
��xA•xB=-4��xA+xB=4k��
��OC•OD+AC•BD=yAyB-xAxB=$\frac{1}{16}$��xAxB��2-xAxB=1+4=5��
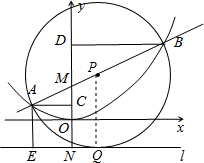
���⣺��ͼ����AB���е�ΪP����P��B��ֱ��l�Ĵ��ߣ�����ֱ�ΪQ��F����PQΪ����AEFB����λ�ߣ��ɣ���֪xA•xB=-4��
xA+xB=4k����yA=kxA+1��yB=kxB+1��
��PQ������AEFB����λ�ߣ�
��PQ=$\frac{AE+BF}{2}$=$\frac{{��y}_{A}+1��+��{y}_{B}+1��}{2}$=$\frac{{y}_{A}+{y}_{B}}{2}$+1=$\frac{k��{x}_{A}+{x}_{B}��}{2}$+2=2��k2+1����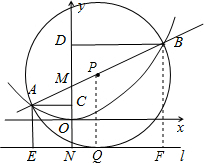
��Rt��ACM�пɵã�
AM=$\sqrt{{AC}^{2}+{MC}^{2}}$=$\sqrt{{x}_{A}^{2}+��1-{y}_{A}��^{2}}$=$\sqrt{{x}_{A}^{2}+{k}^{2}{x}_{A}^{2}}$=-xA•$\sqrt{1+{k}^{2}}$��
ͬ������Rt��BDM�У�
��BM=xB•$\sqrt{1+{k}^{2}}$��
��AB=AM+BM=$\sqrt{1+{k}^{2}}$•��xB-xA����
��AB2=��1+k2��[��xA+xB��2-4xAxB]=��1+k2����16k2+16����
��AB=4��1+k2����PQ=$\frac{1}{2}$AB��
��PQ��l��
����ABΪֱ����Բ��ֱ��l���У�
���� ���⿼�����Բ���ۺ��⣬�漰������ϵ���Ĺ�ϵ�����ɶ��������ε���λ�߶�����֪ʶ���ڽ��III��ʱҪע���������ν����⣮


 ���Ǽ���С����ϵ�д�
���Ǽ���С����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
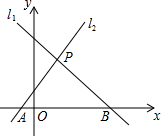 ��ͼ����ֱ��l1��y=-x+4��l2��y=2x+1�ཻ�ڵ�P����x��ֱ��ཻ��A��B���㣮
��ͼ����ֱ��l1��y=-x+4��l2��y=2x+1�ཻ�ڵ�P����x��ֱ��ཻ��A��B���㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
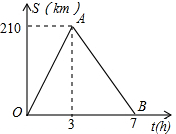 С����A�س�����;�о���C�أ���B�أ�����B�غ�����ԭ·���أ�����A�صľ���S��ǧ�ף�������ʱ��t��Сʱ��֮��ĺ�����ϵ��ͼ��ʾ����С��ǰ�����ξ�����Cʱ�����2$\frac{1}{3}$Сʱ����ôA��C����֮�����Ϊ140ǧ�ף�
С����A�س�����;�о���C�أ���B�أ�����B�غ�����ԭ·���أ�����A�صľ���S��ǧ�ף�������ʱ��t��Сʱ��֮��ĺ�����ϵ��ͼ��ʾ����С��ǰ�����ξ�����Cʱ�����2$\frac{1}{3}$Сʱ����ôA��C����֮�����Ϊ140ǧ�ף��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com