
分析 将已知等式左边通分并利用同分母分式的减法法则计算,得到n-m=7mn,代入所求式子中计算,即可求出值.
解答 解:∵$\frac{1}{m}$-$\frac{1}{n}$=7,
∴$\frac{n-m}{mn}$=7,即n-m=7mn,
则原式=$\frac{5mn-4(n-m)}{(n-m)-3mn}$=$\frac{5mn-28mn}{7mn-3mn}$=$\frac{-23mn}{4mn}$=-$\frac{23}{4}$.
故答案是:-$\frac{23}{4}$.
点评 此题考查了分式的化简求值,分式的加减运算关键是通分,通分的关键是找最简公分母;分式的乘除运算关键是约分,约分的关键是找公因式,约分时,分式的分子分母出现多项式,应将多项式分解因式后再约分.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
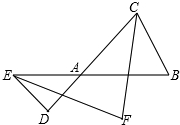 如图,E和D分别在△ABC的边BA和CA的延长线上,CF,EF分别平分∠ACB和∠AED,若∠B=60°,∠D=40°,则∠F的大小是50.
如图,E和D分别在△ABC的边BA和CA的延长线上,CF,EF分别平分∠ACB和∠AED,若∠B=60°,∠D=40°,则∠F的大小是50.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com