
ЁОЬтФПЁПФГЩЬГЁМЦЛЎЙКНјМзЁЂввСНжжЩЬЦЗЃЌвбжЊЙКНјМзЩЬЦЗ2МўКЭввЩЬЦЗ1МўЙВаш50дЊЃЌЙКНјМзЩЬЦЗ1МўКЭввЩЬЦЗ2МўЙВаш70дЊ.
ЃЈ1ЃЉЧѓМзЁЂввСНжжЩЬЦЗУПМўЕФНјМлЗжБ№ЪЧЖрЩйдЊЃП
ЃЈ2ЃЉЩЬГЁОіЖЈМзЩЬЦЗвдУПМў20дЊГіЪлЃЌввЩЬЦЗвдУПМў50дЊГіЪлЃЌЮЊТњзуЪаГЁашЧѓЃЌашЙКНјМзЁЂввСНжжЩЬЦЗЙВ60МўЃЌШєвЊБЃжЄЛёРћВЛЕЭгк1000дЊЃЌдђМзЩЬЦЗзюЖрФмЙКНјЖрЩйМўЃП
ЁОД№АИЁПЃЈ1ЃЉМзЁЂввСНжжЩЬЦЗУПМўЕФНјМлЗжБ№ЪЧ10дЊЃЌ30дЊЃЛЃЈ2ЃЉМзЩЬЦЗзюЖрФмЙКНј20Мў.
ЁОНтЮіЁП
ЃЈ1ЃЉЩшМзЁЂввСНжжЩЬЦЗУПМўЕФНјМлЗжБ№ЪЧxЁЂyдЊЃЌИљОнЁАЙКНјМзЩЬЦЗ2МўКЭввЩЬЦЗ1МўЙВаш50дЊЃЌЙКНјМзЩЬЦЗ1МўКЭввЩЬЦЗ2МўЙВаш70дЊЁБ"СаЗНГЬзщЧѓНтПЩЕУЃЛ
ЃЈ2ЃЉЩшЙКНјМзЩЬЦЗmМўЃЌввЩЬЦЗЃЈ60-mЃЉМўЃЌИљОнЁАЛёРћВЛЕЭгк1000дЊЁБСаВЛЕШЪНЧѓНтПЩЕУ.
ЃЈ1ЃЉЩшМзЁЂввСНжжЩЬЦЗУПМўЕФНјМлЗжБ№ЪЧ![]() дЊЁЂ
дЊЁЂ![]() дЊЃЌ
дЊЃЌ
ИљОнЬтвтЃЌЕУЃК![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
Д№ЃКМзЁЂввСНжжЩЬЦЗУПМўЕФНјМлЗжБ№ЪЧ10дЊЃЌ30дЊЃЛ
ЃЈ2ЃЉЩшЙКНјМзЩЬЦЗ![]() МўЃЌввЩЬЦЗ
МўЃЌввЩЬЦЗ![]() МўЃЌ
МўЃЌ
ИљОнЬтвтЃЌЕУЃК![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
Д№ЃКМзЩЬЦЗзюЖрФмЙКНј20Мў.


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌЖўДЮКЏЪ§![]() ЕФЭМЯѓгыxжсЕФвЛИіНЛЕуЮЊAЃЈ3ЃЌ0ЃЉЃЌСэвЛИіНЛЕуЮЊBЃЌЧвгыyжсНЛгкЕуCЃЎ
ЕФЭМЯѓгыxжсЕФвЛИіНЛЕуЮЊAЃЈ3ЃЌ0ЃЉЃЌСэвЛИіНЛЕуЮЊBЃЌЧвгыyжсНЛгкЕуCЃЎ

ЃЈ1ЃЉЧѓmЕФжЕЃЛ
ЃЈ2ЃЉЧѓЕуBЕФзјБъЃЛ
ЃЈ3ЃЉИУЖўДЮКЏЪ§ЭМЯёЩЯгавЛЕуDЃЈxЃЌyЃЉЃЈЦфжа![]() ЃЌ
ЃЌ![]() ЃЉЃЌЪЙ
ЃЉЃЌЪЙ![]() ЃЌЧѓЕуDЕФзјБъЃЎ
ЃЌЧѓЕуDЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
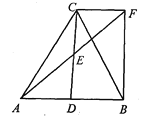
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌDЪЧABЕФжаЕуЃЌEЪЧCDЕФжаЕуЃЌ Й§ЕуCзїCF//ABНЛAEЕФбгГЄЯпгкЕуFЃЌСЌНгBFЃЎ
(1) ЧѓжЄЃКDBЃНCFЃЛ
(2) ШчЙћACЃНBCЃЌЪдХаЖЯЫФБпаЮBDCFЕФаЮзДЃЌВЂжЄУїФуЕФНсТлЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮABCDжаЃЌЕуEЪЧBCЕФжаЕуЃЌСЌНгDEЃЌЙ§ЕуAзїAGЁЭEDНЛDEгкЕуFЃЌНЛCDгкЕуGЃЎ
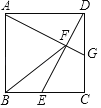
ЃЈ1ЃЉжЄУїЃКЁїADGЁеЁїDCEЃЛЃЈ2ЃЉСЌНгBFЃЌжЄУїЃКABЃНFBЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
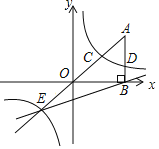
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌAЕуЕФзјБъЮЊЃЈaЃЌ6ЃЉЃЌABЁЭxжсгкЕуBЃЌcosЁЯOABЈT![]() ЃЌЗДБШР§КЏЪ§y=
ЃЌЗДБШР§КЏЪ§y=![]() ЕФЭМЯѓЕФвЛжЇЗжБ№НЛAOЁЂABгкЕуCЁЂDЃЎбгГЄAOНЛЗДБШР§КЏЪ§ЕФЭМЯѓЕФСэвЛжЇгкЕуEЃЎвбжЊЕуDЕФзнзјБъЮЊ
ЕФЭМЯѓЕФвЛжЇЗжБ№НЛAOЁЂABгкЕуCЁЂDЃЎбгГЄAOНЛЗДБШР§КЏЪ§ЕФЭМЯѓЕФСэвЛжЇгкЕуEЃЎвбжЊЕуDЕФзнзјБъЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓжБЯпEBЕФНтЮіЪНЃЛ
ЃЈ3ЃЉЧѓSЁїOEBЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПе§ЗНаЮ![]() жаЃЌ
жаЃЌ![]() ЪЧ
ЪЧ![]() жаЕуЃЌЕу
жаЕуЃЌЕу![]() ДгЕу
ДгЕу![]() ГіЗЂби
ГіЗЂби![]() ЕФТЗЯпдШЫйдЫЖЏЃЌЕНЕу
ЕФТЗЯпдШЫйдЫЖЏЃЌЕНЕу![]() ЭЃжЙЃЌЕу
ЭЃжЙЃЌЕу![]() ДгЕу
ДгЕу![]() ГіЗЂЃЌби
ГіЗЂЃЌби![]() ТЗЯпдШЫйдЫЖЏЃЌ
ТЗЯпдШЫйдЫЖЏЃЌ![]() ЁЂ
ЁЂ![]() СНЕуЭЌЪБГіЗЂЃЌЕу
СНЕуЭЌЪБГіЗЂЃЌЕу![]() ЕФЫйЖШЪЧЕу
ЕФЫйЖШЪЧЕу![]() ЫйЖШЕФ
ЫйЖШЕФ![]() БЖ
БЖ![]() ЃЌЕБЕу
ЃЌЕБЕу![]() ЭЃжЙЪБЃЌЕу
ЭЃжЙЪБЃЌЕу![]() вВЭЌЪБЭЃжЙдЫЖЏЃЌЩш
вВЭЌЪБЭЃжЙдЫЖЏЃЌЩш![]() УыЪБЃЌе§ЗНаЮ
УыЪБЃЌе§ЗНаЮ![]() гы
гы![]() жиЕўВПЗжЕФУцЛ§ЮЊ
жиЕўВПЗжЕФУцЛ§ЮЊ![]() ЃЌ
ЃЌ![]() Йигк
Йигк![]() ЕФКЏЪ§ЙиЯЕШчЭМ2ЫљЪОЃЌдђ
ЕФКЏЪ§ЙиЯЕШчЭМ2ЫљЪОЃЌдђ
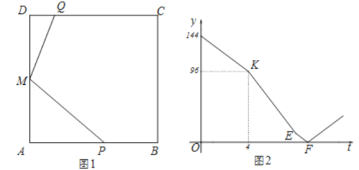
ЃЈ1ЃЉЧѓе§ЗНаЮБпГЄ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉЧѓЭМ2жаЯпЖЮ![]() ЫљдкжБЯпЕФНтЮіЪН.
ЫљдкжБЯпЕФНтЮіЪН.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAЃЌBЕФзјБъЗжБ№ЮЊЃЈ6ЃЌ6ЃЉЃЌЃЈ6ЃЌ0ЃЉЃЌХзЮяЯпyЃНЉЃЈxЉmЃЉ2+nЕФЖЅЕуPдкелЯпOAЉABЩЯдЫЖЏЃЎ
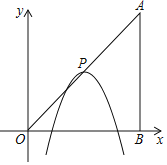
ЃЈ1ЃЉЕБЕуPдкЯпЖЮOAЩЯдЫЖЏЪБЃЌХзЮяЯпyЃНЉЃЈxЉmЃЉ2+nгыyжсНЛЕузјБъЮЊЃЈ0ЃЌcЃЉЃЎ
ЂйгУКЌmЕФДњЪ§ЪНБэЪОnЃЌ
ЂкЧѓcЕФШЁжЕЗЖЮЇЃЎ
ЃЈ2ЃЉЕБХзЮяЯпyЃНЉЃЈxЉmЃЉ2+nОЙ§ЕуBЪБЃЌЧѓХзЮяЯпЫљЖдгІЕФКЏЪ§БэДяЪНЃЛ
ЃЈ3ЃЉЕБХзЮяЯпгыЁїABOЕФБпгаШ§ИіЙЋЙВЕуЪБЃЌжБНгаДГіЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЖўДЮКЏЪ§![]() ЕФЭМЯѓгыxжсЗжБ№НЛгкAЃЈ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкЕуC.
ЕФЭМЯѓгыxжсЗжБ№НЛгкAЃЈ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкЕуC.

ЃЈ1ЃЉЧѓДЫЖўДЮКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉЕуDЮЊХзЮяЯпЕФЖЅЕуЃЌЪдХаЖЯЁїBCDЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉдкХзЮяЯпЕФЖдГЦжсЩЯЪЧЗёДцдквЛЕуЃаЃЌЪЙЕУЃаC+ЃаAзюЖЬЃПШєЃаЕуДцдкЃЌЧѓГіЃаЕуЕФзјБъЃЛШєЃаЕуВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЦНааЫФБпаЮABCDдкЦНУцжБНЧзјБъЯЕжаЃЌADЃН6ЃЌШєOAЁЂOBЕФГЄЪЧЙигкxЕФвЛдЊЖўДЮЗНГЬx2Љ7x+12ЃН0ЕФСНИіИљЃЌЧвOAЃОOBЃЎ
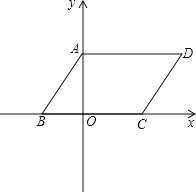
ЃЈ1ЃЉЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЃЈ2ЃЉШєEЮЊxжсЩЯЕФЕуЃЌЧвSЁїAOEЃН![]() ЃЌЧѓОЙ§DЁЂEСНЕуЕФжБЯпЕФНтЮіЪНЃЌВЂХаЖЯЁїAOEгыЁїDAOЪЧЗёЯрЫЦЃП
ЃЌЧѓОЙ§DЁЂEСНЕуЕФжБЯпЕФНтЮіЪНЃЌВЂХаЖЯЁїAOEгыЁїDAOЪЧЗёЯрЫЦЃП
ЃЈ3ЃЉШєЕуMдкЦНУцжБНЧзјБъЯЕФкЃЌдђдкжБЯпABЩЯЪЧЗёДцдкЕуFЃЌЪЙвдAЁЂCЁЂFЁЂMЮЊЖЅЕуЕФЫФБпаЮЮЊСтаЮЃПШєДцдкЃЌЧыжБНгаДГіFЕуЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com