
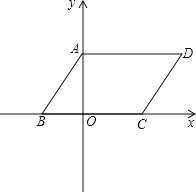
����Ŀ����ͼ��ƽ���ı���ABCD��ƽ��ֱ������ϵ�У�AD��6����OA��OB�ij��ǹ���x��һԪ���η���x2��7x+12��0������������OA��OB��
��1����![]() ��ֵ��
��ֵ��
��2����EΪx���ϵĵ㣬��S��AOE��![]() ����D��E�����ֱ�ߵĽ���ʽ�����жϡ�AOE���DAO�Ƿ����ƣ�
����D��E�����ֱ�ߵĽ���ʽ�����жϡ�AOE���DAO�Ƿ����ƣ�
��3������M��ƽ��ֱ������ϵ�ڣ�����ֱ��AB���Ƿ���ڵ�F��ʹ��A��C��F��MΪ������ı���Ϊ���Σ������ڣ���ֱ��д��F������ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��![]() ����2��y��
����2��y��![]() x��
x��![]() ��y��
��y��![]() x+
x+![]() ����AOE�ס�DAO����3�����ڣ����������ĵ����ĸ���F1����3��0����F2��3��8����F3����
����AOE�ס�DAO����3�����ڣ����������ĵ����ĸ���F1����3��0����F2��3��8����F3����![]() ����
����![]() ����F4����
����F4����![]() ��
��![]() ����
����
��������
��1����һԪ���η������OA��OB�ij��ȣ������ù��ɶ������AB�ij��ȣ��ٴ�����㼴�ɣ�
��2���ȸ��������ε���������E�����꣬������ƽ���ı��εĶԱ���ȵ����������D�����꣬Ȼ�����ô���ϵ�������ֱ�ߵĽ���ʽ���ֱ�����������μ�ֱ�ǵ�����Ӧ�ߵıȣ������ȣ��������������ƣ��������ƣ�
��3���������ε����ʣ���AC��AF���ڱ߲��ҵ�F������AB��������BA������������Լ�AC��AF�ֱ��ǶԽ��ߵ�����ֱ���������㣮
�⣺��1��x2��7x+12��0��
��x��3����x��4����0��
��x��3��0��x��4��0��
���x1��3��x2��4��
��OA��OB��
��OA��4��OB��3��
�ڡ�AOB�У�AB��![]() ��
��![]() ��5��
��5��
��sin��ABC��![]() ��
��
��2���������⣬��E��x��0������
S��AOE��![]() ��OA��x��
��OA��x��![]() ��4x��
��4x��![]() ��
��
���x��![]() ��
��
��E��![]() ��0����
��0����![]() ��0����
��0����
���ı���ABCD��ƽ���ı��Σ�
���D�������ǣ�6��4����
�辭��D��E�����ֱ�ߵĽ���ʽΪy��kx+b��
����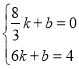 ��
��
��� 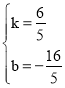 ��
��
�����ʽΪy��![]() x��
x��![]() ��
��
��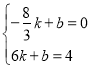 ��
��
��� ��
��
����ʽΪ�� y��![]() x+
x+![]()
�ڡ�AOE���DAO�У� ![]() ��
��
![]() ��
��
��![]() ��
��
�֡ߡ�AOE����OAD��90�㣬
���AOE�ס�DAO��
��3�����ݼ�������ݣ�OB��OC��3��
��AOƽ�֡�BAC��
��AC��AF���ڱߣ���F������AB��ʱ��AF��AC��5��
���Ե�F��B�غϣ�
��F����3��0����
��AC��AF���ڱߣ���F������BA��ʱ��MӦ��ֱ��AD�ϣ���FC��ֱƽ��AM��
��F��3��8����
��AC�ǶԽ���ʱ����AC��ֱƽ����L��AC����ʽΪy����![]() x+4��ֱ��L����
x+4��ֱ��L����![]() ��2������kֵΪ
��2������kֵΪ![]() ��ƽ���ڻ��ഹֱ������ֱ��kֵ�˻�Ϊ��1����
��ƽ���ڻ��ഹֱ������ֱ��kֵ�˻�Ϊ��1����
L����ʽΪy��![]() x+
x+![]() ������ֱ��L��ֱ��AB�㣬
������ֱ��L��ֱ��AB�㣬
��F����![]() ����
����![]() ����
����
��AF�ǶԽ���ʱ����C��AB���ߣ�����ΪN�����ݵȻ������CN��![]() �����ɶ����ó���AN��
�����ɶ����ó���AN��![]() ����A����N�ĶԳƵ㼴ΪF��AF��
����A����N�ĶԳƵ㼴ΪF��AF��![]() ����F��y�ᴹ�ߣ�����ΪG��FG��
����F��y�ᴹ�ߣ�����ΪG��FG��![]() ��
��
��F����![]() ��
��![]() ����
����
�������������������ĵ����ĸ���F1����3��0����F2��3��8����F3����![]() ����
����![]() ����F4����
����F4����![]() ��
��![]() ����
����




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳��ƻ������ס���������Ʒ����֪��������Ʒ2��������Ʒ1������50Ԫ����������Ʒ1��������Ʒ2������70Ԫ.
��1����ס���������Ʒÿ���Ľ��۷ֱ��Ƕ���Ԫ��
��2���̳���������Ʒ��ÿ��20Ԫ���ۣ�����Ʒ��ÿ��50Ԫ���ۣ�Ϊ�����г������蹺���ס���������Ʒ��60������Ҫ��֤����������1000Ԫ�������Ʒ����ܹ������ټ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
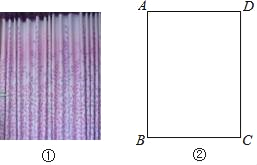
����Ŀ����ͼ�٣�������������ָ���մ�����ʵ�ʿ��Ƚ�����������һ�������ӿ�������������֮��Ĵ�������������Ʈ�ݡ��鶯��Ч�������У������ȵ�1.5��Ϊƽ���壬�����ȵ�2��Ϊ�������壮��ͼ�ڣ�С��Ĵ����ʳ����Σ������Ŀ��ȣ�AD���ȸ߶ȣ�AB������0.5m��ij�ִ����ļ۸�Ϊ120Ԫ/m2������Բ�������ķ�ʽ�������ִ�������ƽ����ķ�ʽ���ö�180Ԫ����С�䴰���Ŀ�����߶ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
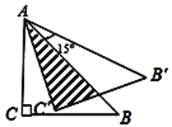
����Ŀ��������Rt��ABC�Ƶ�A��ʱ����ת15���õ���AB��C������AC=1����ͼ����Ӱ�������Ϊ��������
A.![]() B.3
B.3![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����к����������˾������һ���ļ���װ��ͨ��ʵ���̵�������̵�����;���������ۣ�����һ��ʱ��ù�˾��������Ʒ�����������������Ϊ��30��ĸ��ٵ��飬����ʵ���̵����������y1���ټ�����ʱ��t��tΪ��������λ���죩�IJ��ֶ�Ӧֵ�����ʾ��
ʱ��t���죩 | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
��������yt���ټ��� | 0 | 25 | 40 | 45 | 40 | 25 | 0 |
��1��������һ�κ��������κ����ͷ����������У�ѡ����ʵĺ����ܷ�ӳy1��t�ı仯���ɣ������y1��t�ĺ�����ϵʽ��������t��ȡֵ��Χ��
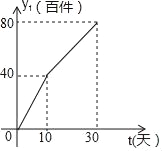
��2�������̵����������y2���ټ�����ʱ��t��tΪ��������λ���죩�Ĺ�ϵ��ͼ��ʾ����y2��t�ĺ�����ϵʽ����д���Ա���t��ȡֵ��Χ��
��3���ڸ��ٵ����30���У���ʵ���̵�������̵������������Ϊy���ټ�������y��t�ĺ�����ϵʽ����tΪ��ֵʱ������������y�ﵽ��������ʱ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
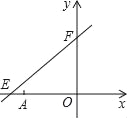
����Ŀ����ͼ��ֱ��y=![]() x+6��x�ᡢy��ֱ��ཻ�ڵ�E��F����A������Ϊ����6��0����P��x��y����ֱ��y=
x+6��x�ᡢy��ֱ��ཻ�ڵ�E��F����A������Ϊ����6��0����P��x��y����ֱ��y=![]() x+6��һ�����㣮
x+6��һ�����㣮
��1���ڵ�P�˶������У���д����OPA�����s��x�ĺ�����ϵʽ��
��2����P�˶���ʲôλ�ã���OPA�����Ϊ![]() �������ʱ��P�����ꣻ
�������ʱ��P�����ꣻ
��3����P��EF�Ĵ��߷ֱ�x�ᡢy����C��D���Ƿ���������ĵ�P��ʹ��COD�ա�FOE�������ڣ�ֱ��д����ʱ��P�����꣨��Ҫ��д�����̣����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪һ�κ���y��ax+b��a��bΪ������a��0����ͼ����x�ᣬy��ֱ��ڵ�A��B�����뷴��������y��![]() ��kΪ������k��0����ͼ���ڵڶ������ڽ��ڵ�C����CD��x���ڣ���OA��OD��
��kΪ������k��0����ͼ���ڵڶ������ڽ��ڵ�C����CD��x���ڣ���OA��OD��![]() OB��3��
OB��3��
��1����һ�κ����뷴���������Ľ���ʽ��
��2���۲�ͼ��ֱ��д������ʽ0��ax+b��![]() �Ľ⼯��
�Ľ⼯��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵������� A��B ������Ʒ�������� A ����Ʒ 5 ���� B ����Ʒ 4 ���� 300 Ԫ������ A ����Ʒ 6 ���� B ���� Ʒ 8 ���� 440 Ԫ.
��1���� A��B ������Ʒÿ���Ľ��۷ֱ�Ϊ����Ԫ��
��2�������̵�ÿ���� 1 �� A ����Ʒ�ɻ��� 8 Ԫ��ÿ���� 1 �� B ����Ʒ�ɻ��� 6 Ԫ�����̵������� A��B ������ Ʒ�� 50 ��������������Ʒȫ���۳����ܻ������� 344 Ԫ�������ٹ������ټ� A ��Ʒ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
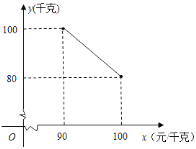
����Ŀ��ij��Ҷר���꾭��һ�������̲裬ÿǧ�˳ɱ�![]() Ԫ����������Ա���鷢�֣�ÿ�µ�������
Ԫ����������Ա���鷢�֣�ÿ�µ�������![]() ��ǧ�ˣ������۵���
��ǧ�ˣ������۵���![]() ��Ԫ/ǧ�ˣ�֮�������ͼ��ʾ�ı仯���ɣ�
��Ԫ/ǧ�ˣ�֮�������ͼ��ʾ�ı仯���ɣ�
![]() ��ÿ��������
��ÿ��������![]() �����۵���
�����۵���![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
![]() ��ij�¸ò�Ҷ�����������̲�������
��ij�¸ò�Ҷ�����������̲�������![]() Ԫ��������²�Ҷ�����۵���
Ԫ��������²�Ҷ�����۵���![]() Ϊ����Ԫ��
Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com