
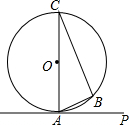
 如图所示,PA是⊙O的切线,切点为A,∠PAB是切线AP与弦AB的夹角,∠C是$\widehat{AB}$所对的圆周角.
如图所示,PA是⊙O的切线,切点为A,∠PAB是切线AP与弦AB的夹角,∠C是$\widehat{AB}$所对的圆周角.分析 (1)根据切线的性质得出∠CAB+∠BAP=90°,再利用直径得出∠ACB+∠CAB=90°证明即可;
(2)连接AO并延长交圆于E,连接BE,根据直径所对的圆周角是直角,可以得到∠E+∠EAB=90°;再根据AB是切线可以得到∠EAB+∠1=90°,所以∠E=∠1,最后根据等弧所对的圆周角相等就可以的得到所要的结论.
解答 解:(1)∠C=∠BAP,理由如下:
∵PA是⊙O的切线,切点为A,
∴∠CAP=90°,
∴∠CAB+∠BAP=90°,
∵AC是直径,
∴∠ACB+∠CAB=90°,
∴∠C=∠BAP;
(2)如图,作直径AE,连接EB,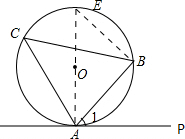
∠C=∠BAP
∵AE是⊙O的直径,
∴∠EAB+∠E=∠EBA=90°;
又∵AB是⊙O的切线,
∴∠EAB+∠1=90°,
∴∠1=∠E;
∴∠C=∠1.
∴∠C=∠BAP.
点评 本题综合运用了切线的性质、等角的余角相等以及圆周角定理的推论,熟记定理是解题的关键.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源:2016-2017学年江苏省扬州市七年级下学期第一次月考数学试卷(解析版) 题型:填空题
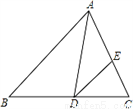
如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是_______.
查看答案和解析>>
科目:初中数学 来源:2017届山东省日照市莒县第三协作区九年级3月学业水平模拟考试数学试卷(解析版) 题型:判断题
除夕夜中央电视台举办的“2016年春节联欢晚会”受到广泛的关注.某组织就“2016年春节联欢晚会”节目的喜爱程度,在三峡广场进行了问卷调查,并对问卷调查的结果分为“非常喜欢”、“比较喜欢”、“感觉一般”、“不太喜欢”四个等级,分别记作A、B、C、D;根据调查结果绘制出如图所示的扇形统计图(未完成)和条形统计图(未完成),请结合图中所给信息解答下列问题
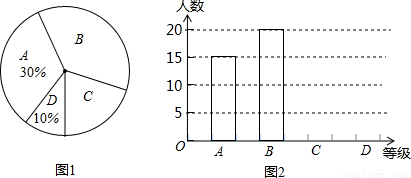
(1)本次被调查对象共有 人;被调查者“不太喜欢”有 人。
(2)将扇形统计图和条形统计图补充完整;
(3)在“非常喜欢”调查结果里有人为80后,其中3男2女,在这5人中,该组织打算随机选2位进行采访,请你用列表法或树状图法求出所选2位恰好都为男性的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且AB=15cm,BC=20cm,CA=25cm.
如图,△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且AB=15cm,BC=20cm,CA=25cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
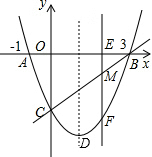 如图,抛物线与x轴交于点A(-1,0)、点B(3,0),交y轴于点C(0,-3),点M为线段BC上一动点,过点M作x轴的垂线,交x轴于点E,交抛物线于点F
如图,抛物线与x轴交于点A(-1,0)、点B(3,0),交y轴于点C(0,-3),点M为线段BC上一动点,过点M作x轴的垂线,交x轴于点E,交抛物线于点F查看答案和解析>>
科目:初中数学 来源: 题型:填空题
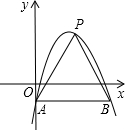 如图,在平面直角坐标系中,抛物线y=-(x-2)2+3与y轴交于点A,过点A与x轴平行的直线交抛物线于另一点B.点P是直线AB上方的抛物线上一点,设点P的横坐标为m,则△PAB的面积S的取值范围为0<S≤8.
如图,在平面直角坐标系中,抛物线y=-(x-2)2+3与y轴交于点A,过点A与x轴平行的直线交抛物线于另一点B.点P是直线AB上方的抛物线上一点,设点P的横坐标为m,则△PAB的面积S的取值范围为0<S≤8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
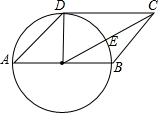 如图,在?ABCD中,AB=$\sqrt{2}$AD,以AB为直径的⊙O经过点D,连接OC交⊙O于点E.
如图,在?ABCD中,AB=$\sqrt{2}$AD,以AB为直径的⊙O经过点D,连接OC交⊙O于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com