
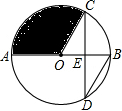
 如图,AB是⊙O的直径,弦CD交AB于点E,且E是CD的中点,∠CDB=30°,CD=6$\sqrt{3}$,则阴影部分面积为( )
如图,AB是⊙O的直径,弦CD交AB于点E,且E是CD的中点,∠CDB=30°,CD=6$\sqrt{3}$,则阴影部分面积为( )| A. | π | B. | 3π | C. | 6π | D. | 12π |
分析 根据题意得出△COB是等边三角形,进而得出CD⊥AB,再利用垂径定理以及锐角三角函数关系得出CO的长,进而结合扇形面积求出答案.
解答 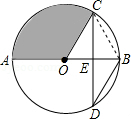 解:连接BC,
解:连接BC,
∵∠CDB=30°,
∴∠COB=60°,
∴∠AOC=120°,
又∵CO=BO,
∴△COB是等边三角形,
∵E为OB的中点,
∴CD⊥AB,
∵CD=6$\sqrt{3}$,
∴EC=3$\sqrt{3}$,
∴sin60°×CO=3$\sqrt{3}$,
解得:CO=6,
故阴影部分的面积为:$\frac{120π×{6}^{2}}{360}$=12π.
故选D.
点评 此题主要考查了垂径定理以及锐角三角函数和扇形面积求法等知识,正确得出CO的长是解题关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
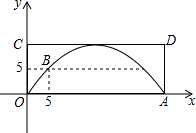 如图,一座抛物线型拱桥,桥面CD与水面平行,在正常水位时桥下水面宽OA为30米,拱桥B处为警戒水位标识,点B到OC的水平距离和它到水面OA的距离都为5米.
如图,一座抛物线型拱桥,桥面CD与水面平行,在正常水位时桥下水面宽OA为30米,拱桥B处为警戒水位标识,点B到OC的水平距离和它到水面OA的距离都为5米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
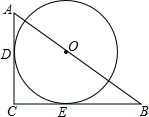 如图,⊙O与Rt△ACB的两直角边AC、BC相切,切点分别为D、E两点,且圆心O在斜边AB上.
如图,⊙O与Rt△ACB的两直角边AC、BC相切,切点分别为D、E两点,且圆心O在斜边AB上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 排数(x) | 1 | 2 | 3 | 4 | … |
| 座位数(y) | 50 | 53 | 56 | 59 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com