
【题目】请阅读以下材料,并解决问题:
配方法是数学中重要的一种思想方法. 它是指将一个式子或一个式子的某一部分通过恒等变形化为完全平方式或几个完全平方式的和的方法. 这种方法常被用到代数恒等变形中,并结合非负数的意义来解决一些问题.
(例1)把二次三项式![]() 进行配方.
进行配方.
解:![]() -4.
-4.
(例2)已知![]() ,求
,求![]() 和
和![]() 的值.
的值.
解:由已知得:
![]() ,
,
即![]() ,
,
所以![]() ,
,
所以![]() .
.
(1)若![]() 可配方成
可配方成![]() (
(![]() 为常数),求
为常数),求![]() 和
和![]() 的值;
的值;
(2)已知实数![]() 满足
满足![]() ,求
,求![]() 的最大值;
的最大值;
(3)已知![]() 为正实数,且满足
为正实数,且满足![]() 和
和![]() ,试判断以
,试判断以![]() 为三边的长的三角形的形状,并说明理由.
为三边的长的三角形的形状,并说明理由.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)以
;(3)以![]() ,
,![]() ,
,![]() 为三边的长的三角形是等腰直角三角形,理由详见解析.
为三边的长的三角形是等腰直角三角形,理由详见解析.
【解析】
(1)把![]() 配方后,与
配方后,与![]() 比较即可;
比较即可;
(2)把![]() 变形为
变形为![]() ,再把右边配方,即可求出
,再把右边配方,即可求出![]() 的最大值;
的最大值;
(3)把![]() 因式分解可得三角形是以
因式分解可得三角形是以![]() ,
,![]() ,a+b为三边的长的等腰三角形;把所给两个式子相加可得以三角形是以
,a+b为三边的长的等腰三角形;把所给两个式子相加可得以三角形是以![]() ,
,![]() ,a+b为三边的长的直角三角形,从而可判定三角形是以
,a+b为三边的长的直角三角形,从而可判定三角形是以![]() ,
,![]() ,a+b为三边的长的等腰直角三角形.
,a+b为三边的长的等腰直角三角形.
(1)因为![]() .
.
所以![]() ,
,![]() .
.
(2)解法一:
由![]() 可得:
可得:
![]() .
.
![]() .
.
因为![]()
![]() ,
,
即当![]() 时,
时,![]() 的最大值为
的最大值为![]() .
.
解法二:
由![]() 可得:
可得:
![]() ,
,
移项,得
![]() .
.
因为![]() ,所以
,所以![]() ,
,
即当![]() 时,
时,![]() 的最大值为
的最大值为![]() .
.
(3)以![]() ,
,![]() ,a+b为三边的长的三角形是等腰直角三角形,理由如下:
,a+b为三边的长的三角形是等腰直角三角形,理由如下:
由![]() 可得:
可得:
![]() ,
,
![]() ,
,
![]() ,
,
因为![]() ,
,![]() ,
,![]() 都为正数,
都为正数,
所以![]() ,
,![]() ,
,
所以![]() ,即以
,即以![]() ,
,![]() ,a+b为三边的长的三角形是等腰三角形,
,a+b为三边的长的三角形是等腰三角形,
![]() ………①
………①
![]() ………②
………②
由①![]() ②得:
②得:
![]() ,
,
![]() ,
,
![]() .
.
即以![]() ,
,![]() ,a+b为三边的长的三角形是直角三角形,
,a+b为三边的长的三角形是直角三角形,
所以以![]() ,
,![]() ,a+b为三边的长的三角形是等腰直角三角形.
,a+b为三边的长的三角形是等腰直角三角形.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】如图,已知正比例函数y=3x的图象与反比例函数y=![]() 的图象交于点A(1,m)和点B.
的图象交于点A(1,m)和点B.
(1)求m的值和反比例函数的解析式.
(2)观察图象,直接写出使正比例函数的值大于反比例函数的值的自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某体育用品商店,购买50根跳绳和80个毽子共用1120元,购买30根跳绳和50个毽子共用680元.
(1)跳绳、毽子的单价各是多少元?
(2)该店在“元旦”节期间开展促销活动,所有商品按同样的折数打折销售.节日期间购买100根跳绳和100个毽子只需1700元,该店的商品按原价的几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 的解析式为
的解析式为![]() ,直线
,直线![]() 的解析式为
的解析式为![]() ,与
,与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,点
,点![]() ,直线
,直线![]() 与
与![]() 交于点
交于点![]() .
.

(1)求点![]() ,点
,点![]() ,点
,点![]() 的坐标,并求出
的坐标,并求出![]() 的面积;
的面积;
(2)若直线 ![]() 上存在点
上存在点![]() (不与
(不与![]() 重合),满足
重合),满足![]() ,请求出点
,请求出点![]() 的坐标;
的坐标;
(3)在![]() 轴右侧有一动直线平行于
轴右侧有一动直线平行于![]() 轴,分别与
轴,分别与![]() ,
,![]() 交于点
交于点![]() ,且点
,且点![]() 在点
在点![]() 的下方,
的下方,![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为等腰直角三角形?若存在,请直接写出满足条件的点
为等腰直角三角形?若存在,请直接写出满足条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是∠AOB的平分线上的一点,PC⊥OA,PD⊥OB,垂足分别为C,D.下列结论 不一定成立的是( )

A.∠AOP=∠BOPB.PC=PD
C.∠OPC=∠OPDD.OP=PC+PD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:

①因为a>0,所以函![]() 数
数![]() 有最大值;
有最大值;
②该函数图象关于直线![]() 对称;
对称;
③当![]() 时,函数y的值大于0;
时,函数y的值大于0;
④当![]() 时,函数y的值都等于0.
时,函数y的值都等于0.
其中正确结论的个数是
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
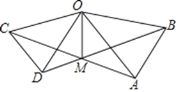
【题目】如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC.其中正确的是____________________________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com