
分析 (1)求出y=-$\sqrt{3}$x+m与x轴的交点B的坐标,根据B、C两点坐标求出解析式即可;
(2)过P作x轴的垂线交AB于K,先证明△AKP∽△MPB,得$\frac{AP}{PM}$=$\frac{PK}{PB}$=$\sqrt{3}$,再证明△AOP∽△PMN,得$\frac{AP}{PM}$=$\frac{AO}{PN}$=$\frac{OP}{MN}$=$\sqrt{3}$,从而求出PN的长;
(3)分两种情况:OP=PM或MP=MO,分类讨论即可.
解答 解(1)∵y=-$\sqrt{3}$x+m
∴A(0,m) B($\frac{\sqrt{3}}{3}$m,0)
∴tan∠OAB=$\frac{BO}{AO}$=$\frac{\frac{\sqrt{3}}{3}m}{m}$=$\frac{\sqrt{3}}{3}$,
∴∠BAO=30
又∵∠OAB=∠OBC=30°,OC=$\sqrt{3}$
∴OB=3,AO=3$\sqrt{3}$,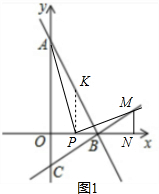
∴B(3,0),A(0,3$\sqrt{3}$),
设BC的解为y=kx+b,
解设$\left\{\begin{array}{l}{3k+b=0}\\{b=-\sqrt{3}}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{k=\frac{\sqrt{3}}{3}}\\{b=-\sqrt{3}}\end{array}\right.$,
∴y=$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$;
(2)如图1,过P作x轴的垂线交AB于K,
∵AP⊥PM
∴∠APM=∠KPB=90°,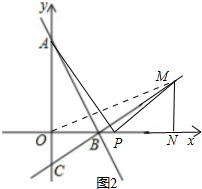
∴∠APK=∠BPM,
又∵∠AKP=∠PBM=150°,
∴△AKP∽△MPB,
∴$\frac{AP}{PM}$=$\frac{PK}{PB}$=$\sqrt{3}$,
又∵∠AOP=∠MNP=90°,∠PAO=∠MPN,
∴△AOP∽△PMN,
∴$\frac{AP}{PM}$=$\frac{AO}{PN}$=$\frac{OP}{MN}$=$\sqrt{3}$
∴$\frac{3\sqrt{3}}{PN}$=$\sqrt{3}$,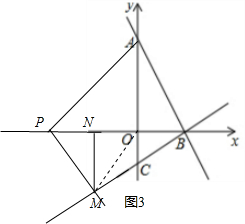
∴PN=3;
(3)①如图2,①当OP=PM时,PM=OP=t,PN=3,
∵$\frac{AP}{PM}=\frac{PK}{PB}=\frac{OP}{MN}=\sqrt{3}$,
∴MN=$\frac{\sqrt{3}}{3}$t,
在Rt△PMN中 PM2=PN2+MN2
t2=9+($\frac{\sqrt{3}}{3}$t)2 t=$±\frac{3\sqrt{6}}{2}$
②如图3,当MP=MO时,则ON=$\frac{1}{2}$PO,
∴-$\frac{t}{2}$=3,
∴t=-6.
∴t为$±\frac{3\sqrt{6}}{2}$或-6时,△PMO是以PM为腰的等腰三角形.
点评 本题主要考查了一次函数的综合应用、锐角三角函数、三角形相似的判定与性质、等腰三角形的判定与性质、勾股定理.熟练地运用数形结合,发现图形中的相似三角形是解决问题的关键.


科目:初中数学 来源: 题型:解答题
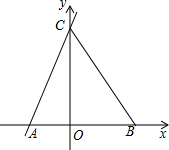 如图,已知点(-2,0),B(3,0),C(0,6),连接BC.
如图,已知点(-2,0),B(3,0),C(0,6),连接BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
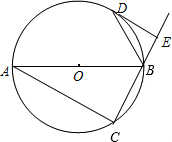 已知:如图,△ABC是⊙O的内角三角形,△ABC的外角平分线BD交⊙O于D,DE与⊙O相切,交CB的延长线于E.
已知:如图,△ABC是⊙O的内角三角形,△ABC的外角平分线BD交⊙O于D,DE与⊙O相切,交CB的延长线于E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
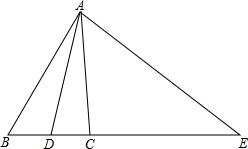 如图所示,在△ABC中,∠EAD=∠EDA,∠EAC=∠B.
如图所示,在△ABC中,∠EAD=∠EDA,∠EAC=∠B.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
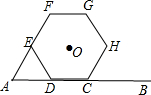 如图,已知线段AB=10,点D从A点开始沿AB边向右运动,以AD为边向上作正△ADE,再以DE为边向右作正六边形DEFGHC,点C恰好落在线段AB上,当C与B重合时运动结束,则正六边形的中心O的运动路径长为5$\sqrt{3}$,点B与点O的最短距离为5.
如图,已知线段AB=10,点D从A点开始沿AB边向右运动,以AD为边向上作正△ADE,再以DE为边向右作正六边形DEFGHC,点C恰好落在线段AB上,当C与B重合时运动结束,则正六边形的中心O的运动路径长为5$\sqrt{3}$,点B与点O的最短距离为5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com