
 如图,在Rt△ABO中,∠AOB=90°,OA=OB=4,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线长PQ的最小值是( )
如图,在Rt△ABO中,∠AOB=90°,OA=OB=4,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线长PQ的最小值是( )| A. | A$\sqrt{6}$ | B. | $\sqrt{7}$ | C. | 2$\sqrt{2}$ | D. | 3 |
分析 连接OP,OQ,由PQ为圆O的切线,利用切线的性质得到OQ与PQ垂直,利用勾股定理列出关系式,由OP最小时,PQ最短,根据垂线段最短得到OP垂直于AB时最短,利用面积法求出此时OP的值,再利用勾股定理即可求出PQ的最短值.
解答 解:连接OP、OQ,如图所示,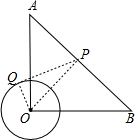
∵PQ是⊙O的切线,
∴OQ⊥PQ,
根据勾股定理知:PQ2=OP2-OQ2,
∴当PO⊥AB时,线段PQ最短,
∵在Rt△AOB中,OA=OB=4,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=4$\sqrt{2}$,
∴S△AOB=$\frac{1}{2}$OA•OB=$\frac{1}{2}$AB•OP,即OP=$\frac{OA•OB}{AB}$=2$\sqrt{2}$,
∴PQ=$\sqrt{O{P}^{2}-O{Q}^{2}}$=$\sqrt{(2\sqrt{2})^{2}-{1}^{2}}$=$\sqrt{7}$,
故选B.
点评 此题考查了切线的性质,勾股定理的应用,熟练掌握切线的性质是解本题的关键,注意:圆的切线垂直于过切点的半径.


科目:初中数学 来源:2017届江苏省东台市第四教育联盟九年级下学期第一次月考数学试卷(解析版) 题型:填空题
在平面直角坐标系xOy中,已知反比例函数y= (k≠0)满足:当x<0时,y随x的增大而减小.若该反比例函数的图象与直线y=﹣x+
(k≠0)满足:当x<0时,y随x的增大而减小.若该反比例函数的图象与直线y=﹣x+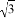 k都经过点P,且|OP|=
k都经过点P,且|OP|=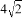 ,则实数k的值为__.
,则实数k的值为__.
查看答案和解析>>
科目:初中数学 来源:2017届辽宁省大石桥市中考模拟(一)数学试卷(解析版) 题型:单选题
下列事件是必然事件的是( )
A. 任意购买一张电影票,座位号是奇数 B. 打开电视,正在播出“奔跑吧,兄弟”
C. 13名同学中至少有两名同学出生的月份相同 D. 抛掷一枚硬币,反面朝上
查看答案和解析>>
科目:初中数学 来源:2015-2016学年内蒙古巴彦淖尔市临河区七年级下学期期末考试数学试卷(解析版) 题型:单选题
直角坐标系中,点P(x,y)在第二象限,且P 到x 轴、y 轴距离分别为3,7,则P 点坐标为( )
A. (-3,7) B. (-7,3) C. (3,7) D. (7,3)
查看答案和解析>>
科目:初中数学 来源:2015-2016学年内蒙古巴彦淖尔市临河区七年级下学期期末考试数学试卷(解析版) 题型:单选题
下列4对数值中是方程2x﹣y=1的解的是( )
A. 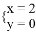 B.
B. 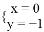 C.
C. 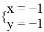 D.
D. 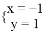
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数y=x2-4x+3.
已知二次函数y=x2-4x+3.| x | … | … | |||||
| y | … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com