
| 型号 | 数量(台) | 进价(元/台) |
| A | 10 | 150元 |
| B | 5 | 350元 |
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 步行人数为30人 | B. | 骑车人数占总人数的10% | ||
| C. | 该班总人数为50人 | D. | 乘车人数是骑车人数的40% |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
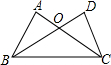 如图,△ABC和△DCB中,∠A=∠D=90°,边AC与DB相交于点O,要使△ABC≌△DCB,则需要添加的一个条件是AB=DC.(写出一种情况即可)
如图,△ABC和△DCB中,∠A=∠D=90°,边AC与DB相交于点O,要使△ABC≌△DCB,则需要添加的一个条件是AB=DC.(写出一种情况即可)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-y)2=(y-x)2 | B. | (x+6)(x-6)=x2-6 | ||
| C. | (x+y)=x2+y2 | D. | (3x-y)(-3x+y)=9x2-y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.09×107 | B. | 2.09×108 | C. | 20.9×107 | D. | 209×107 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com