
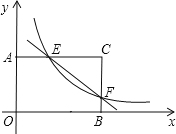
【题目】在矩形AOBC中,OB=6,OA=4,分别以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系.F是边BC上一点(不与B、C两点重合),过点F的反比例函数![]() (k>0)图象与AC边交于点E.
(k>0)图象与AC边交于点E.
(1)请用k的表示点E,F的坐标;
(2)若△OEF的面积为9,求反比例函数的解析式.
【答案】(1)E(![]() ,4),F(6,
,4),F(6, ![]() );(2) 反比例函数的解析式为y=
);(2) 反比例函数的解析式为y= ![]() .
.
【解析】试题分析:(1)易得E点的纵坐标为4,F点的横坐标为6,把它们分别代入反比例函数y=![]() (k>0)即可得到E点和F点的坐标;
(k>0)即可得到E点和F点的坐标;
(2)分别用矩形面积和能用图中的点表示出的三角形的面积表示出所求的面积,解方程即可求得k的值.
试题解析:(1)E(![]() ,4),F(6,
,4),F(6, ![]() );
);
(2)∵E,F两点坐标分别为E(![]() ,4),F(6,
,4),F(6, ![]() ),
),
∴S△ECF=![]() ECCF=
ECCF=![]() (6-
(6-![]() )(4-
)(4-![]() ),
),
∴S△EOF=S矩形AOBC-S△AOE-S△BOF-S△ECF
=24- ![]() k-
k- ![]() k- S△ECF
k- S△ECF
=24-k -![]() (6-
(6-![]() )(4-
)(4-![]() ),
),
∵△OEF的面积为9,
∴24-k -![]() (6-
(6-![]() )(4-
)(4-![]() )=9,
)=9,
整理得, ![]() =6,
=6,
解得k =12.
∴反比例函数的解析式为=![]()
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】到x轴的距离等于2的点组成的图形是
A. 过点0,2且与x轴平行的直线
B. 过点2,0且与y轴平行的直线
C. 过点0,2且与x轴平行的直线
D. 分别过0,2和0,2且与x轴平行的两条直线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣2,y1)、B(1,y2)在二次函数y=x2+2x+2的图象上,y1与y2的大小关系为( )
A.y1>y2B.y1=y2C.y1<y2D.y1≤y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b、c是三角形的三边长,如果满足 ![]() =0,则三角形的形状是( )
=0,则三角形的形状是( )
A.底与边不相等的等腰三角形
B.等边三角形
C.钝角三角形
D.直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3 . 若S1+S2+S3=15,则S2的值是( )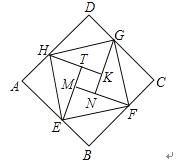
A.3
B.![]()
C.5
D.![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
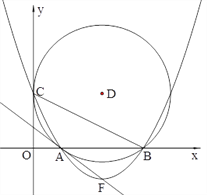
【题目】如图24,在平面直角坐标系中,圆D与![]() 轴相切于点C(0,4),与
轴相切于点C(0,4),与![]() 轴相交于A、B两点,且AB=6
轴相交于A、B两点,且AB=6
(1)D点的坐标是 ,圆的半径为 ;
(2)求经过C、A、B三点的抛物线所对应的函数关系式;
(3)设抛物线的顶点为F,试证明直线AF与圆D相切;
(4)在![]() 轴下方的抛物线上,是否存在一点N,使
轴下方的抛物线上,是否存在一点N,使![]() 面积最大,最大面积是多少?并求出
面积最大,最大面积是多少?并求出![]() 点坐标.
点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”.
(1)说明方程x2-3x+2=0是倍根方程;
(2)说明:若(x-2)(mx+n)=0是倍根方程,则4m2+5mn+n2=0;
(3)如果方程ax2+bx+c=0是倍根方程,且相异两点M(1+t,s),N(4-t,s)都在抛物线y=ax2+bx+c上,试说明方程ax2+bx+c=0的一个根为![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com