
【题目】如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”.
(1)说明方程x2-3x+2=0是倍根方程;
(2)说明:若(x-2)(mx+n)=0是倍根方程,则4m2+5mn+n2=0;
(3)如果方程ax2+bx+c=0是倍根方程,且相异两点M(1+t,s),N(4-t,s)都在抛物线y=ax2+bx+c上,试说明方程ax2+bx+c=0的一个根为![]() .
.
【答案】(1)理由见解析;(2)理由见解析;(3)理由见解析.
【解析】试题分析:(1)解得方程后即可利用倍根方程的定义进行判断;
(2)根据(x-2)(mx+n)=0是倍根方程,从而得到m+n=0,4m+n=0,进而得到4m2+5mn+n2=(4m+n)(m+n)=0;
(3)由方程ax2+bx+c=0是倍根方程,得到x1=3x2,由相异两点M(1+t,s),N(4-t,s)都在抛物线y=ax2+bx+c上,通过抛物线对称轴求得x1的值.
试题解析:(1)解方程x2-3x+2=0得:x1=2,x2=1,
∴方程x2-3x+2=0是倍根方程.
(2)∵(x-2)(mx+n)=0是倍根方程,且x1=2,x2=-![]() ,
,
∴![]() =-1,或
=-1,或![]() =-4,
=-4,
∴m+n=0,4m+n=0,
∵4m2+5mn+n2=(4m+n)(m+n)=0,
(3)∵方程ax2+bx+c=0是倍根方程,
∴设x1=2x2,
∵相异两点M(1+t,s),N(4-t,s)都在抛物线y=ax2+bx+c上,
∴抛物线的对称轴x=![]() ,
,
∴x1+x2=5,
∴x2+2x2=5,
∴x2=![]() .
.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
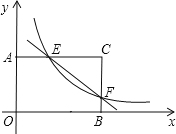
【题目】在矩形AOBC中,OB=6,OA=4,分别以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系.F是边BC上一点(不与B、C两点重合),过点F的反比例函数![]() (k>0)图象与AC边交于点E.
(k>0)图象与AC边交于点E.
(1)请用k的表示点E,F的坐标;
(2)若△OEF的面积为9,求反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算正确的是( )
A. 3a3·2a2=6a6 B. 3x·3x4=9x4
C. 2x3·4x5=8x8 D. 5b7·5b7=10b14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 是边
是边![]() 上一点.
上一点.
(![]() )如图
)如图![]() ,若
,若![]() 交
交![]() 延长线于点
延长线于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,求证:
,求证: ![]() ;
;
(![]() )如图
)如图![]() ,若
,若![]() 为线段
为线段![]() 上一点,且
上一点,且![]() ,
, ![]() 的延长线交
的延长线交![]() 于
于![]() ,请判断线段
,请判断线段![]() 与
与![]() 的关系,并证明你的猜想.
的关系,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在反比例函数 ![]() (x>0)的图象上,有点P1、P2、P3、P4 , 它们的横坐标依次是1、2、3、4,分别过这些点作x轴与y轴的垂线,若图中所构成的阴影部分的面积从左到右依次为S1、S2、S3 , 则S1+S2+S3= .
(x>0)的图象上,有点P1、P2、P3、P4 , 它们的横坐标依次是1、2、3、4,分别过这些点作x轴与y轴的垂线,若图中所构成的阴影部分的面积从左到右依次为S1、S2、S3 , 则S1+S2+S3= . 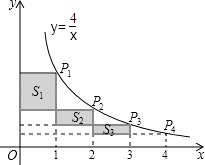
查看答案和解析>>
科目:初中数学 来源: 题型:
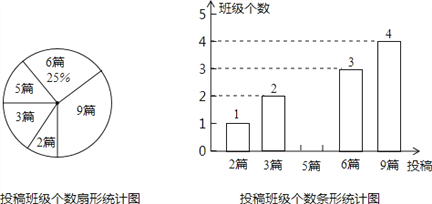
【题目】为积极响应市政府提出的“建设美丽南宁”的号召,我市某校在八,九年级开展征文活动,校学生会对这两个年级各班内的投稿情况进行统计,并制成了如图所示的两幅不完整的统计图.
(1)求扇形统计图中投稿篇数为2所对应的扇形的圆心角的度数:
(2)求该校八,九年级各班在这一周内投稿的平均篇数,并将该条形统计图补充完整.
(3)在投稿篇数为9篇的四个班级中,八,九年级各有两个班,校学生会准备从这四个班中选出两个班参加全市的表彰会,请你用列表法或画树状图的方法求出所选两个班正好不在同一年级的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com