
【题目】已知:在![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 是边
是边![]() 上一点.
上一点.
(![]() )如图
)如图![]() ,若
,若![]() 交
交![]() 延长线于点
延长线于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,求证:
,求证: ![]() ;
;
(![]() )如图
)如图![]() ,若
,若![]() 为线段
为线段![]() 上一点,且
上一点,且![]() ,
, ![]() 的延长线交
的延长线交![]() 于
于![]() ,请判断线段
,请判断线段![]() 与
与![]() 的关系,并证明你的猜想.
的关系,并证明你的猜想.

【答案】(![]() )
)![]() ;(
;(![]() )
)![]() 且
且![]() .
.
【解析】试题分析:(1)由等腰直角三角形的性质得到:AD=CD,再证明△MAD≌△ECD,即可得到结论.
(2)证明△ACE≌△CBG,得到CE=BG,∠ACE=∠CBG,再证明BG⊥CE即可.
试题解析:(![]() )证明:∵点D是AB中点,AC=BC,∠ACB=90°,∴CD⊥AB,∠ACD=∠DAC=45°,∴AD=CD.
)证明:∵点D是AB中点,AC=BC,∠ACB=90°,∴CD⊥AB,∠ACD=∠DAC=45°,∴AD=CD.
又∵AH⊥CE,∴∠HAE+∠AEH=90°,
又∵∠CED+∠ECD=90°,∠AEH=∠CED(对顶角相等),∴∠HAE=∠ECD,
在△MAD和△ECD中.∵∠MAD=∠ECD,AD=CD,∠ADM=∠CDE=90°,
∴△MAD≌△ECD(ASA ),∴DE=DM.
(2)BG=CE且BG⊥CE.证明如下:
∵点D是AB中点,AC=BC,∠ACB=90°,∴CD⊥AB,∠CAD=∠BCD=45°.
在△ACE和△CBG中,∵AC=BC,∠CAE=∠BCG=45°,AE=CG,∴△ACE≌△CBG(SAS ),∴CE=BG,∠ACE=∠CBG.
又∵∠ACB=90°,∴∠ACE+∠ECB=90°,∴∠CBG+∠ECB=90°,∴在△BCF中,∠FCB+∠CBF=90°,∴∠CFB=90°,∴BF⊥CE即BG⊥CE,
综上所述,BG=CE且BG⊥CE.


科目:初中数学 来源: 题型:
【题目】已知a、b、c是三角形的三边长,如果满足 ![]() =0,则三角形的形状是( )
=0,则三角形的形状是( )
A.底与边不相等的等腰三角形
B.等边三角形
C.钝角三角形
D.直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b、c满足|a﹣ ![]() |+
|+ ![]() +(c﹣4
+(c﹣4 ![]() )2=0.
)2=0.
(1)求a、b、c的值;
(2)判断以a、b、c为边能否构成三角形?若能构成三角形,此三角形是什么形状?并求出三角形的面积;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
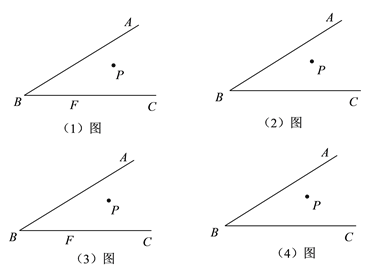
【题目】动手操作:请按要求作图.(规范作图,保留作图痕迹即可,不要求尺规作图)
(![]() )如图(
)如图(![]() ),
),![]() 是
是![]() 内一定点,
内一定点, ![]() 为射线
为射线![]() 边上一定点,请在射线
边上一定点,请在射线![]() 上找一点
上找一点![]() ,使得
,使得![]() 最小.
最小.
(![]() )如图(
)如图(![]() ),
),![]() 是
是![]() 内一定点,点
内一定点,点![]() 、
、![]() 分别为射线
分别为射线![]() 、
、![]() 边上两个动点,请作出使得
边上两个动点,请作出使得![]() 最小的
最小的![]() 点和
点和![]() 点.
点.
(![]() )如图(
)如图(![]() ),
),![]() 是
是![]() 内一定点,点
内一定点,点![]() 、
、![]() 分别为射线
分别为射线![]() 、
、![]() 边上两个动点,请作出使得
边上两个动点,请作出使得![]() 最小的
最小的![]() 点和
点和![]() 点.
点.
拓展应用:
(![]() )如图(
)如图(![]() ),
),![]() 为锐角三角形,
为锐角三角形, ![]() ,
, ![]() ,
, ![]() 的面积为
的面积为![]() ,点
,点![]() 、
、![]() 、
、![]() 分别为
分别为![]() 三边
三边![]() 、
、![]() 、
、![]() 上的三个动点,请在图中作出满足条件的周长最小的
上的三个动点,请在图中作出满足条件的周长最小的![]() ,并求出
,并求出![]() 周长的最小值.
周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”.
(1)说明方程x2-3x+2=0是倍根方程;
(2)说明:若(x-2)(mx+n)=0是倍根方程,则4m2+5mn+n2=0;
(3)如果方程ax2+bx+c=0是倍根方程,且相异两点M(1+t,s),N(4-t,s)都在抛物线y=ax2+bx+c上,试说明方程ax2+bx+c=0的一个根为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
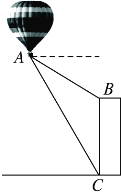
【题目】如图,热气球的探测器显示,从热气球A看一栋大楼顶部B的俯角为30°,看这栋大楼底部C的俯角为60°,热气球A的高度为240米,求这栋大楼的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于受猪流感的影响,4月初某地猪肉价格大幅度下调,下调后每斤猪肉价格是原价格的![]() ,原来用60元买到的猪肉下调后可多买2斤.4月中旬,经专家研究证实,猪流感不是由猪传染,很快更名为甲型H1N1流感.因此,猪肉价格4月底开始回升,经过两个月后,猪肉价格上调为每斤14.4元.
,原来用60元买到的猪肉下调后可多买2斤.4月中旬,经专家研究证实,猪流感不是由猪传染,很快更名为甲型H1N1流感.因此,猪肉价格4月底开始回升,经过两个月后,猪肉价格上调为每斤14.4元.
(1)求4月初猪肉价格下调后每斤多少元?
(2)求5、6月份猪肉价格的月平均增长率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com