
【题目】如图,在反比例函数 ![]() (x>0)的图象上,有点P1、P2、P3、P4 , 它们的横坐标依次是1、2、3、4,分别过这些点作x轴与y轴的垂线,若图中所构成的阴影部分的面积从左到右依次为S1、S2、S3 , 则S1+S2+S3= .
(x>0)的图象上,有点P1、P2、P3、P4 , 它们的横坐标依次是1、2、3、4,分别过这些点作x轴与y轴的垂线,若图中所构成的阴影部分的面积从左到右依次为S1、S2、S3 , 则S1+S2+S3= . 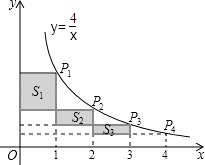
科目:初中数学 来源: 题型:
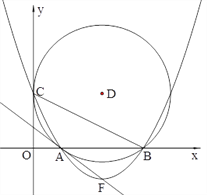
【题目】如图24,在平面直角坐标系中,圆D与![]() 轴相切于点C(0,4),与
轴相切于点C(0,4),与![]() 轴相交于A、B两点,且AB=6
轴相交于A、B两点,且AB=6
(1)D点的坐标是 ,圆的半径为 ;
(2)求经过C、A、B三点的抛物线所对应的函数关系式;
(3)设抛物线的顶点为F,试证明直线AF与圆D相切;
(4)在![]() 轴下方的抛物线上,是否存在一点N,使
轴下方的抛物线上,是否存在一点N,使![]() 面积最大,最大面积是多少?并求出
面积最大,最大面积是多少?并求出![]() 点坐标.
点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”.
(1)说明方程x2-3x+2=0是倍根方程;
(2)说明:若(x-2)(mx+n)=0是倍根方程,则4m2+5mn+n2=0;
(3)如果方程ax2+bx+c=0是倍根方程,且相异两点M(1+t,s),N(4-t,s)都在抛物线y=ax2+bx+c上,试说明方程ax2+bx+c=0的一个根为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)观察思考:如图,线段AB上有两个点C、D,请分别写出以点A、B、C、D为端点的线段,并计算图中共有多少条线段;
(2)模型构建:如果线段上有m个点(包括线段的两个端点),则该线段上共有多少条线段?请说明你结论的正确性;
(3)拓展应用:8位同学参加班上组织的象棋比赛,比赛采用单循环制(即每两位同学之间都要进行一场比赛),那么一共要进行多少场比赛?
请将这个问题转化为上述模型,并直接应用上述模型的结论解决问题.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将点P(-2,1)向右平移3个单位,再向下平移4个单位得到点P′,则点P′的坐标是( )
A. (2,4) B. (1,-3) C. (1,5) D. (-5,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,是假命题的是( )
A. 三角形的外角大于任一内角
B. 能被2整除的数,末尾数字必是偶数
C. 两直线平行,同旁内角互补
D. 相反数等于它本身的数是0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com