
| 1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
| 甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
| 乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
分析 (1)根据每人踢100个以上(含100)为优秀和图表给出的数据即可得出甲班和乙班的优秀率;
(2)根据中位数的定义先把数据从小到大排列,再找出最中间的数即可;
(3)先求出甲班和乙班的平均数,再根据方差公式即可得出答案;
(4)根据甲班的优秀率高于乙班,甲班的成绩从中位数看也高于乙班,甲班的方差小于乙班,成绩更稳定,从而得出答案.
解答 解:(1)甲班的优秀率为:$\frac{3}{5}$×100%=60%,乙班的优秀率为$\frac{2}{5}$×100%=40%;
(2)把甲班比赛数据从小到大排列为:89,98,100,103,110,最中间的数是100,则甲班比赛数据的中位数为100;
把乙班比赛数据从小到大排列为:89,95,97,100,119,最中间的数是97,则乙班比赛数据的中位数为97;
故答案为:100,97;
(3)甲班的平均数是:(89+98+100+103+110)÷5=100(个);
乙班的平均数是:(89+95+97+100+119)÷5=100(个),
甲的方差是:$\frac{1}{5}$[(89-100)2+(98-100)2+(100-100)2+(103-100)2+(110-100)2]=46.8,
乙的方差是:$\frac{1}{5}$[(89-100)2+(95-100)2+(97-100)2+(100-100)2+(119-100)2]=103.2,
则甲班的方差较小;
故答案为:甲;
(4)甲班,理由:甲班的优秀率高于乙班,甲班的成绩从中位数看也高于乙班,甲班的方差小于乙班,成绩更稳定.
点评 本题考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.


科目:初中数学 来源: 题型:解答题
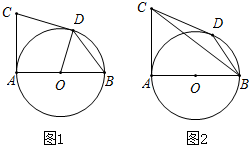
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
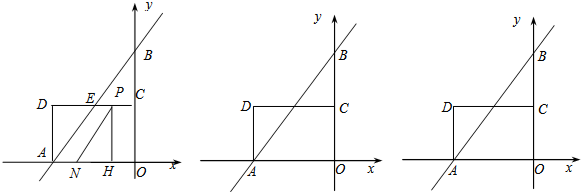
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
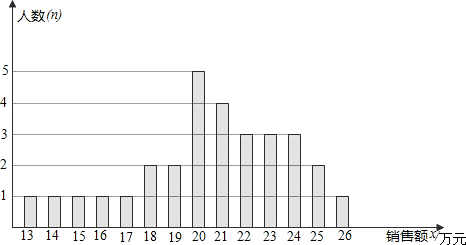
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
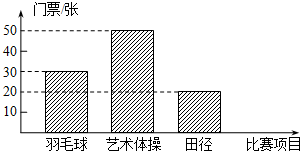 2010年5月20日上午10时起,2010年广州亚运会门票全面发售.下表为抄录广州亚运会官方网公布的三类比赛的部分门票价格,如图为某公司购买的门票种类、数量所绘制成的条形统计图.
2010年5月20日上午10时起,2010年广州亚运会门票全面发售.下表为抄录广州亚运会官方网公布的三类比赛的部分门票价格,如图为某公司购买的门票种类、数量所绘制成的条形统计图.| 比赛项目 | 票价(元/张) |
| 羽毛球 | 400 |
| 艺术体操 | 240 |
| 田径 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com