Question

【题目】如图，平面直角坐标系中，△ABC的顶点都在网格点上，其中，C点坐标为（1，2）.

（1）写出点A、B的坐标：A　 　，B　 　 ；

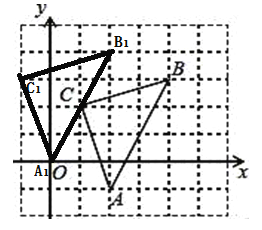
（2）将△ABC先向左平移2个单位长度，再向上平移1个单位长度，得到△A1B1C1，画出△A1B1C1；

（3）若AB边上有一点M（a，b），平移后对应的点M1的坐标为________________；

（4）求△ABC的面积．

Answer 1

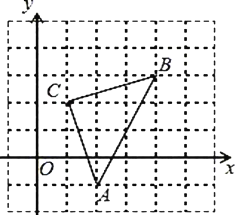
【答案】（1）A（2，-1），B（4，3）；（2）详见解析；（3）M1的坐标为(a-2，b+1)；（4）5.

【解析】

（1）根据点A、点B在坐标系中的位置，直接写出它们的坐标即可；（2）由于△ABC先向左平移2个单位长度，再向上平移1个单位长度，得到△A1B1C1，则分别把点A、点B、点C的横坐标减去2，纵坐标加上1即可得到点A1、点B1、点C1的坐标，顺次连接即可画出△A1B1C1；（3）由点M到点M1可知应把点M先向左平移2的单位，再向上平移1个单位，把点M的横坐标减去2，纵坐标加上1即可得到点M1的坐标；（4）利用S△ABC=S矩形BEDF-S△ADC-S△ABE-S△BCF进行计算即可；

（1）A（2，-1），B（4,3）；

（2）如图所示：

（3）M1的坐标为(a-2，b+1)；

（4）如图，

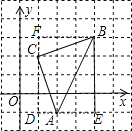
S△ABC=S矩形BEDF-S△ADC-S△ABE-S△BCF==3×4-×3×1-×2×4-×3×1=5.