
分析 先确定直线与坐标轴的交点坐标为(0,b),(-$\frac{b}{k}$,0),利用直线与坐标轴围成的三角形是等腰三角形,所以|b|=|-$\frac{b}{k}$|,解得k=1或k=-1,则把(2,-4)代入y=kx+b得2k+b=-4,然后把k=1或k=-1分别代入可求出对应的b的值,从而得到对应的直线解析式.
解答 解:当x=0时,y=kx+b=b,则直线与y轴的交点坐标为(0,b),
当y=0时,kx+b=0,解得x=-$\frac{b}{k}$,则直线与x轴的交点坐标为(-$\frac{b}{k}$,0),
因为直线与坐标轴围成的三角形是等腰三角形,
所以|b|=|-$\frac{b}{k}$|,解得k=1或k=-1,
把(2,-4)代入y=kx+b得2k+b=-4,
当k=1时,2+b=-4,解得b=-6,此时解析式为y=x-6;
当k=-1时,-2+b=-4,解得b=-2,此时解析式为y=-x-2,
即此直线解析式为y=x-6或y=-x-2.
故答案y=x-6或y=-x-2.
点评 本题考查了待定系数法求一次函数解析式:先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;解方程或方程组,求出待定系数的值,进而写出函数解析式.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 13 | B. | $\sqrt{119}$ | C. | 13或$\sqrt{119}$ | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
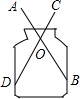 如图,小明家有一个玻璃容器,他想测量一下它的内径是多少?但是他无法将刻度尺伸进去直接测量,于是他把两根长度相等的小木条AB,CD的中点连在一起,木条可以绕中点O自由转动,这样只要测量A,C的距离,就可以知道玻璃容器的内径,你知道其中的道理吗?请说明理由.
如图,小明家有一个玻璃容器,他想测量一下它的内径是多少?但是他无法将刻度尺伸进去直接测量,于是他把两根长度相等的小木条AB,CD的中点连在一起,木条可以绕中点O自由转动,这样只要测量A,C的距离,就可以知道玻璃容器的内径,你知道其中的道理吗?请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com