
【题目】如图,已知⊙O是以BC为直径的△ABC的外接圆,OP∥AC,且与BC的垂线交于点P,OP交AB于点D,BC、PA的延长线交于点E. 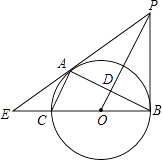
(1)求证:PA是⊙O的切线;
(2)若sinE= ![]() ,PA=6,求AC的长.
,PA=6,求AC的长.
【答案】
(1)证明:连接OA,如图,
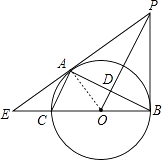
∵AC∥OP,
∴∠ACO=∠POB,∠CAO=∠POA,
又∵OA=OC,
∴∠ACO=∠CAO,
∴∠POA=∠POB,
在△PAO和△PBO中,
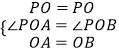 ,
,
∴△PAO≌△PBO(SAS),
∴∠PAO=∠PBO,
又∵PB⊥BC,
∴∠PBO=90°,
∴∠PAO=90°,
∴OA⊥PE,
∴PA是⊙O的切线
(2)解:∵△PAO≌△PBO,
∴PB=PA=6,
在Rt△PBE中,∵sinE= ![]() =
= ![]()
∴ ![]() =
= ![]() ,解得PE=10,
,解得PE=10,
∴AE=PE﹣PA=4,
在Rt△AOE中,sinE= ![]() =
= ![]() ,
,
设OA=3t,则OE=5t,
∴AE= ![]() =4t,
=4t,
∴4t=4,解得t=1,
∴OA=3,
在Rt△PBO中,∵OB=3,PB=6,
∴OP= ![]() =3
=3 ![]() ,
,
∵AC∥OP,
∴△EAC∽△EPO,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴AC= ![]() .
.
【解析】(1)先利用平行线的性质得到∠ACO=∠POB,∠CAO=∠POA,加上∠ACO=∠CAO,则∠POA=∠POB,于是可根据“SAS”判断△PAO≌△PBO,则∠PAO=∠PBO=90°,然后根据切线的判定定理即可得到PA是⊙O的切线;(2)先由△PAO≌△PBO得PB=PA=6,在Rt△PBE中,利用正弦的定义可计算PE=10,则AE=PE﹣PA=4,再在Rt△AOE中,由sinE= ![]() =
= ![]() ,可设OA=3t,则OE=5t,由勾股定理得到AE=4t,则4t=4,解得t=1,所以OA=3;接着在Rt△PBO中利用勾股定理计算出OP=3
,可设OA=3t,则OE=5t,由勾股定理得到AE=4t,则4t=4,解得t=1,所以OA=3;接着在Rt△PBO中利用勾股定理计算出OP=3 ![]() ,然后证明△EAC∽△EPO,再利用相似比可计算出AC.
,然后证明△EAC∽△EPO,再利用相似比可计算出AC.
【考点精析】根据题目的已知条件,利用切线的判定定理的相关知识可以得到问题的答案,需要掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】(1)如图,AC平分∠DAB,∠DCA=∠DAC,试说明AB与CD的位置关系,并予以说明。

(2)如图,在(1)的结论下,AB的下方两点E,F满足:BF平分∠ABE,DF平分∠CDE,若∠DFB=20°,∠CDE=70°,求∠ABE的度数。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的外角∠ACD的平分线CP与∠ABC平分线BP交于点P,若∠BPC=40°,则∠CAP的度数是( )
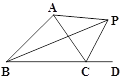
A. 30°; B. 40°; C. 50°; D. 60°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义新运算:![]() .
.
例如:3![]() 2=3(3-2)=3,-1
2=3(3-2)=3,-1![]() 4=-1
4=-1![]() (-1-4)=5.
(-1-4)=5.
(1)请直接写出3![]() a=b的所有正整数解;
a=b的所有正整数解;
(2)已知2![]() a=5b-2m,3
a=5b-2m,3![]() b=5a+m,说明:12a+11b的值与m无关;
b=5a+m,说明:12a+11b的值与m无关;
(3)已知a>1,记M=ab![]() b,N=b
b,N=b![]() ab,试比较M,N的大小.
ab,试比较M,N的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,任意两点A (x1,y1),B (x2,y2)规定运算:①A![]() B=( x1+ x2, y1+ y2);②A
B=( x1+ x2, y1+ y2);②A![]() B= x1 x2+y1 y2③当x1= x2且y1= y2时A=B有下列四个命题:
B= x1 x2+y1 y2③当x1= x2且y1= y2时A=B有下列四个命题:
(1)若A(1,2),B(2,–1),则A![]() B=(3,1),A
B=(3,1),A![]() B=0;
B=0;
(2)若A![]() B=B
B=B![]() C,则A=C;(3)若A
C,则A=C;(3)若A![]() B=B
B=B![]() C,则A=C;
C,则A=C;
(4)对任意点A、B、C,均有(A![]() B )
B ) ![]() C=A
C=A![]() ( B
( B![]() C )成立.其中正确命题的个数为( )
C )成立.其中正确命题的个数为( )
A. 1个 B. 2个 C. 3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你会求(a﹣1)(a2014+a2013+a2012+…+a2+a+1)的值吗?这个问题看上去很复杂,我们可以先考虑简单的情况,通过计算,探索规律:
![]() ;
;
![]() ;
;
![]() .
.
(1)由上面的规律我们可以大胆猜想,得到(a﹣1)(a2014+a2013+a2012+…+a2+a+1)=________
利用上面的结论,求:
(2)22014+22013+22012+…+22+2+1的值是 。
(3)求52014+52013+52012+…+52+5+1的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据提示填空(8分)
如图,EF∥AD,∠1=∠2,∠BAC=80°.将求∠AGD的过程填写完整.

因为EF∥AD
所以∠2=____(____________________________)
又因为∠1=∠2
所以∠1=∠3(______________)
所以AB∥_____(_____________________________)
所以∠BAC+______=180°(_____________________)
因为∠BAC=80° 所以∠AGD=_______
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com