
 如图所示,在△ABC中,AD、BE都是中线,MN平分BE且与AD平行,又知AD、BE、MN将△ABC分成六部分,面积依次是a、b、c、d、e、18,试求a、b、c、d、e的值.
如图所示,在△ABC中,AD、BE都是中线,MN平分BE且与AD平行,又知AD、BE、MN将△ABC分成六部分,面积依次是a、b、c、d、e、18,试求a、b、c、d、e的值. 分析 先利用三角形重心的性质得到AG=2GD,BG=2GE,再利用MN平分BE得到BH:HG:GE=3:1:2,接着证明△BMH∽△BDG,△BHN∽△BGA得到$\frac{HN}{AG}$=$\frac{BH}{BG}$=$\frac{3}{4}$,$\frac{BH}{BG}$=$\frac{MH}{DG}$=$\frac{3}{4}$,则NH=2HM,于是利用等高的三角形面积的比等于底边的比可计算出a=9,再根据相似三角形面积的比等于相似比的平方可计算出b=7,e=14,然后利用等高的三角形面积的等于底边的比计算出d和c的值.
解答 解:∵AD、BE都是中线,
∴点G为△ABC的重心,
∴AG=2GD,BG=2GE,
∵MN平分BE,
∴BH:HG:GE=3:1:2,
∵MN∥AD,
∴△BMH∽△BDG,△BHN∽△BGA,
∴$\frac{HN}{AG}$=$\frac{BH}{BG}$=$\frac{3}{4}$,$\frac{BH}{BG}$=$\frac{MH}{DG}$=$\frac{3}{4}$,
而AG=2GD,
∴NH=2HM,
∴a=$\frac{1}{2}$×18=9,
∵MN∥AD,
∴$\frac{a}{a+b}$=($\frac{3}{4}$)2,即$\frac{9}{9+b}$=$\frac{9}{16}$,解得b=7,
$\frac{18}{18+e}$=($\frac{3}{4}$)2,解得e=14,
∵BG=GE,
∴18+e=2d,即18+14=2d,解得d=16,
∵BD=CD,
∴18+e+a+b=d+c,
即18+14+9+7=16+c,解得c=32.
答:a、b、c、d、e的值分别为9,7,32,16,14.
点评 本题考查了面积及等积变换:同高或等高的三角形面积的比等于底边的比.熟练掌握相似三角形的判定与性质和三角形重心的性质,特别是相似三角形面积的比等于相似比的平方.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
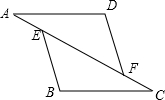 如图,点A,B,F,C在同一直线上,AB=FC,DF=EB,DF∥BE.
如图,点A,B,F,C在同一直线上,AB=FC,DF=EB,DF∥BE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-1)(x+2) | B. | (x-1)(x-2) | C. | (x+1)(x+2) | D. | (x+1)(x-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在研究用火柴摆正方形的问题时,
如图,在研究用火柴摆正方形的问题时,| A. | 小明说的对 | B. | 四位同学说的都对 | ||
| C. | 小明、小凡说得对 | D. | 小亮、小刚说的对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,竖立在点B处的标杆AB高2.5m,站立在点F处的观察者从点E处看到标杆顶A、树顶C在一条直线上.测得BD=9m,FB=3m,EF=1.7m,求树高CD.
如图,竖立在点B处的标杆AB高2.5m,站立在点F处的观察者从点E处看到标杆顶A、树顶C在一条直线上.测得BD=9m,FB=3m,EF=1.7m,求树高CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com