
 如图,△ABC是等边三角形,P是CB延长线上一点,Q是BC延长线上一点,且满足∠PAQ=120°.求证:BC2=PB•QC.
如图,△ABC是等边三角形,P是CB延长线上一点,Q是BC延长线上一点,且满足∠PAQ=120°.求证:BC2=PB•QC. 分析 由∠PAQ=120°,△ABC是等边三角形,易得∠QAC=∠P,∠ABP=∠QCA=180°-60°=120°,即可证得△APB∽△QAC,然后由相似三角形的对应边成比例,证得结论.
解答 证明:∵△ABC是等边三角形,∠PAQ=120°,
∴∠PAB+∠QAC=60°,
∵∠PAB+∠P=∠ABC=60°,
∴∠QAC=∠P,
∵∠ABP=∠QCA=180°-60°=120°,
∴△APB∽△QAC,
∴PB:AC=AB:QC,
∴AB•AC=PB•QC,
∵AB=AC=BC,
∴BC2=PB•QC.
点评 此题考查了相似三角形的判定与性质以及等边三角形的性质.注意证得△APB∽△QAC是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
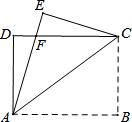 如图,矩形纸片ABCD中,AB=8cm,把矩形纸片沿线AC折叠,点B落在点E处,AE交DC于点F,若AD=$\frac{3}{2}$cm,则AF的长为$\frac{265}{64}$.
如图,矩形纸片ABCD中,AB=8cm,把矩形纸片沿线AC折叠,点B落在点E处,AE交DC于点F,若AD=$\frac{3}{2}$cm,则AF的长为$\frac{265}{64}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一个有理数不是正有理数就是负有理数 | |
| B. | 0是整数但不是正数 | |
| C. | 非正数是指负整数和负分数 | |
| D. | 一个整数不是正整数就是负整数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.844×106 | B. | 3.844×107 | C. | 3.844×108 | D. | 3.844×109 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com