
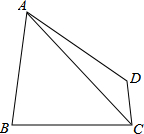
 如图,在四边形ABCD中,AD=AB=BC,连接AC,且∠ACD=30°,tan∠BAC=$\frac{{2\sqrt{3}}}{3}$,CD=3,则AC=6$\sqrt{3}$.
如图,在四边形ABCD中,AD=AB=BC,连接AC,且∠ACD=30°,tan∠BAC=$\frac{{2\sqrt{3}}}{3}$,CD=3,则AC=6$\sqrt{3}$. 分析 过点D、B分别作DE⊥AC,BH⊥AC,垂足分别为E、H,设AC=x,先求得AE(用含x的式子表示)和DE的长,根据勾股定理可表示出AD2,然后根据等腰三角形三线合一的性质可知:AH=$\frac{1}{2}x$,然后根据锐角三角函数的定义可求得HB(用含x的式子表示)的长,根据勾股定理可表示出AB2,然后根据AB=AD,列方程求解即可.
解答 解:过点D、B分别作DE⊥AC,BH⊥AC,垂足分别为E、H,设AC=x.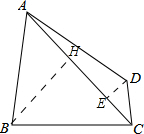
在Rt△CDE中,DC=3,∠DCE=30°,
∴$\frac{DE}{DC}=\frac{1}{2}$,$\frac{EC}{DC}=\frac{\sqrt{3}}{2}$.
∴DE=$\frac{3}{2}$,CE=$\frac{3}{2}\sqrt{3}$.
则AE=x-$\frac{3}{2}\sqrt{3}$,
在Rt△AED中,由勾股定理得:AD2=AE2+DE2=$(x-\frac{3}{2}\sqrt{3})^{2}+\frac{9}{4}$,
∵AB=BC,BH⊥AC,
∴AH=$\frac{1}{2}$AC=$\frac{1}{2}x$,
∵tan∠BAC=$\frac{BH}{AH}=\frac{2\sqrt{3}}{3}$,
∴BH=$\frac{2\sqrt{3}}{3}AH=\frac{\sqrt{3}}{3}x$
在Rt△ABH中,由勾股定理得:AB2=BH2+AH2,
∴$A{B}^{2}=(\frac{1}{2}x)^{2}+(\frac{\sqrt{3}}{3}x)^{2}=\frac{7}{12}{x}^{2}$.
∵AB=AD,
∴$(x-\frac{3}{2}\sqrt{3})^{2}+\frac{9}{4}$=$\frac{7}{12}{x}^{2}$
解得:x1=$6\sqrt{3}$,x2=$\frac{6\sqrt{3}}{5}$(舍去).
∴AC=6$\sqrt{3}$.
点评 本题主要考查的是勾股定理、锐角三角函数、等腰三角形的性质和一元二次方程的应用,利用锐角三角函数的定义和等腰三角形的性质求得AH、BH的长度是解题的关键.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
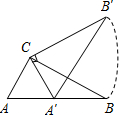 三角板ABC中,∠ACB=90°,∠B=30°,AC=2$\sqrt{3}$,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,则B点转过的路径长为( )
三角板ABC中,∠ACB=90°,∠B=30°,AC=2$\sqrt{3}$,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,则B点转过的路径长为( )| A. | $\frac{3}{2}$π | B. | $\frac{4}{3}$$\sqrt{3}$π | C. | 2π | D. | 3π |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4$\sqrt{2}$+2 | B. | 3 | C. | $\frac{9}{2}$$\sqrt{2}$+2 | D. | 3+2$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com