
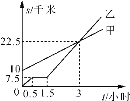
【题目】如图,分别表示甲步行与乙骑自行车(在同一路上)行走的路程s甲,s乙与时间t的关系,观察图象并回答下列问题:
(1)乙出发时,乙与甲相距 千米;
(2)走了一段路程后,乙的自行车发生故障,停下来修车的时间为 小时;
(3)乙从出发起,经过 小时与甲相遇;
(4)乙骑自行车出故障前的速度与修车后的速度一样吗?为什么?
【答案】(1)10;(2)1;(3)3;(4)不一样,理由见解析;
【解析】
(1)根据t=0时甲乙两人的路程差即为两人的距离解答即可;
(2)根据s不变的时间即为修车时间解答即可;
(3)根据两人的函数图象的交点即为相遇,写出时间即可;
(4)利用速度与时间路程的关系解答即可;
解:(1)由图象可知,乙出发时,乙与甲相距10千米.
故答案为:10.
(2)由图象可知,走了一段路程后,乙的自行车发生故障,停下来修车的时间为=1.5-0.5=1小时,
故答案为:1.
(3)图图象可知,乙从出发起,经过3小时与甲相遇.
故答案为:3
(4)乙骑自行车出故障前的速度与修车后的速度不一样.理由如下:
乙骑自行车出故障前的速度![]() =15千米/小时.
=15千米/小时.
与修车后的速度![]() =10千米/小时.
=10千米/小时.
因为15>10,
所以乙骑自行车出故障前的速度与修车后的速度不一样.


科目:初中数学 来源: 题型:
【题目】某届世界杯的小组比赛规则:四个球队进行单循环比赛(每两队赛一场),胜一场得3分,平一场得1分,负一场得0分.某小组比赛结束后,甲、乙、丙、丁四队分别获得第一、二、三、四名,各队的总得分恰好是四个连续奇数,则与乙打平的球队是( )
A. 甲 B. 甲与丁 C. 丙 D. 丙与丁
查看答案和解析>>
科目:初中数学 来源: 题型:
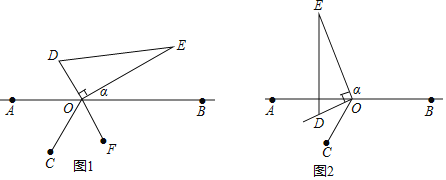
【题目】如图1,点A、O、B在同一直线上,∠AOC=60°,在直线AB另一侧,直角三角形DOE绕直角顶点O逆时针旋转(当OD与OC重合时停止),设∠BOE=α:
(1)如图1,当DO的延长线OF平分∠BOC,∠α=______度;
(2)如图2,若(1)中直角三角形DOE继续逆时针旋转,当OD位于∠AOC的内部,且∠AOD=![]() ∠AOC,∠α=__度;
∠AOC,∠α=__度;
(3)在上述直角三角形DOE的旋转过程中,(∠COD+∠α)的度数是否改变?若不改变,请求出其度数;若改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【新知理解】
如图①,点C在线段AB上,图中共有三条线段AB、AC和BC,若其中有一条线段的长度是另外一条线段长度的2倍,则称点C是线段AB的“巧点”.
线段的中点__________这条线段的“巧点”;(填“是”或“不是”).
若AB = 12cm,点C是线段AB的巧点,则AC=___________cm;
【解决问题】
(3) 如图②,已知AB=12cm.动点P从点A出发,以2cm/s的速度沿AB向点B匀速移动:点Q从点B出发,以1cm/s的速度沿BA向点A匀速移动,点P、Q同时出发,当其中一点到达终点时,运动停止,设移动的时间为t(s).当t为何值时,A、P、Q三点中其中一点恰好是另外两点为端点的线段的巧点?说明理由

![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
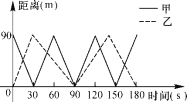
【题目】一游泳池长90 m,甲、乙两人分别从两对边同时向所对的另一边游去,到达对边后,再返回,这样往复数次.图中的实线和虚线分别表示甲、乙与游泳池固定一边的距离随游泳时间变化的情况,根据图形回答:
(1)甲、乙两人分别游了几个来回?
(2)甲游了多长时间?游泳的速度是多少?
(3)在整个游泳过程中,甲、乙两人相遇了几次?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACD中,已知AB⊥CD,且BD>CB,△BCE和△ABD都是等腰直角三角形,王刚同学说有下列全等三角形:
①△ABC≌△DBE;②△ACB≌△ABD;
③△CBE≌△BED;④△ACE≌△ADE.
这些三角形真的全等吗?简要说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算.
(1)﹣7+(﹣8)﹣(﹣18)﹣13
(2)(﹣1)3×(﹣5)﹣(﹣3)÷(﹣![]() )
)
(3)(![]() -
-![]() -
-![]() )÷(﹣
)÷(﹣![]() )
)
(4)﹣12018﹣2![]() ×[13﹣(﹣5)2]
×[13﹣(﹣5)2]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com