
����Ŀ����ͼ1����A��O��B��ͬһֱ���ϣ���AOC=60�㣬��ֱ��AB��һ�ֱ࣬��������DOE��ֱ�Ƕ���O��ʱ����ת����OD��OC�غ�ʱֹͣ�������BOE=����
��1����ͼ1����DO���ӳ���OFƽ�֡�BOC������=______�ȣ�
��2����ͼ2������1����ֱ��������DOE������ʱ����ת����ODλ�ڡ�AOC���ڲ����ҡ�AOD=![]() ��AOC������=__�ȣ�
��AOC������=__�ȣ�
��3��������ֱ��������DOE����ת�����У�����COD+�������Ķ����Ƿ�ı䣿�����ı䣬���������������ı䣬��˵�����ɣ�
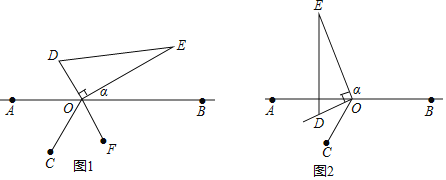
���𰸡���1��30 ����2�� 110����3������COD+�������Ķ������䣬������.
��������
��1���ȸ����ڲ��Ƕ���ͽ�ƽ���ߵĶ��������BOF�Ķ������ٸ�����ǵĶ��弴����������Ķ�����
��2�����ݡ�AOD=![]() ��AOC�á�AOD=20�㣬������ǵĶ���������AOE=70�㣬�ٸ��ݲ��ǵĶ��弴����������Ķ�����
��AOC�á�AOD=20�㣬������ǵĶ���������AOE=70�㣬�ٸ��ݲ��ǵĶ��弴����������Ķ�����
��3�������ܽǵ���360��ɵá�COD+����=360��-��DOE-��BOC����DOE���BOC�Ĵ�С���䣬��֪����COD+�������Ķ���������Ϊ150�㣮
�⣺��1����DO���ӳ���OFƽ�֡�BOC����AOC=60�㣬
���BOF=![]() ��BOC=
��BOC=![]() ��180��-��AOC��=
��180��-��AOC��=![]() ��180��-60�㣩=60�㣬
��180��-60�㣩=60�㣬
�֡ߡ�DOE=90�㣬
�����=90��-��BOF=90��-60��=30�㣮
�ʴ�Ϊ��30
��2����ODλ�ڡ�AOC���ڲ����ҡ�AOD=![]() ��AOCʱ����AOD=
��AOCʱ����AOD=![]() ��
��
�֡ߡ�DOE=90�㣬
���AOE=90��-��AOD=90��-20��=70�㣬
�����=180��-��AOE=180��-70��=110�㣮
�ʴ�Ϊ��110
��3������COD+�������Ķ������䣮
�������£�
�ߣ���COD+������+��DOE+��BOC=360�㣬
�ߡ�DOE=90�㣬��BOC=120�㣬
���COD+����=360��-90��-120��=150�㣮
�ࣨ��COD+�������Ķ���������Ϊ150�㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪���������ε�������������ƽ���ߵĽ��㣬�����������ĵ�һ��ֱ���������ཻ��������֮����߶ΰ���������ηֳ�����ͼ�Σ�����һ��ͼ����ԭ���������ƣ���������߶ν�����������εġ������ߡ���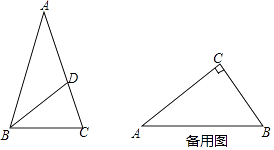
��1���ȱ������Ρ������ߡ�������Ϊ��
��2����ͼ����ABC�У�AB=AC����D��AC�ϣ���BD=BC=AD����֤��BD�ǡ�ABC�ġ������ߡ���
��3����Rt��ABC�У���C=90�㣬AC=4��BC=3��E��F�ֱ��ڱ�AC��BC�ϣ���EF�ǡ�ABC�ġ������ߡ�����EF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵ�У���֪��A����3��0����B��0��4�����ԡ�OAB��������ת�任�����εõ���1����2����3����4��������16��ֱ�Ƕ��������Ϊ��������
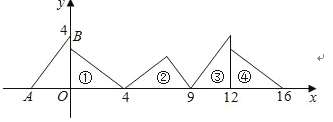
![]()
A. ��60��0�� B. ��72��0�� C. ��67![]() ��
��![]() �� D. ��79
�� D. ��79![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ʵ�н��ݵ���ƶȣ������ͥÿ���õ���������80ǧ��ʱʱ��ʵ�С�������ۡ�����ÿ���õ�������80ǧ��ʱʱ����������ʵ�С���ߵ�ۡ���ȥ��С�ż�4���õ���Ϊ100ǧ��ʱ�������68Ԫ��5���õ���Ϊ120ǧ��ʱ�������88Ԫ���������ۡ���__Ԫ/ǧ��ʱ������ߵ�ۡ���__Ԫ/ǧ��ʱ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ��A��B��C�����ڸ���ϣ�
��1��������ABC����y��ԳƵ���A1B1C1����д����C1�������� ����
��2���ڣ�1���������£�����CC1��AB�ڵ�D��������D����ֱ��д��CD�ij���
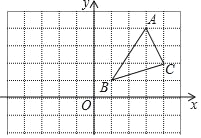
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ƽ��ֱ������ϵxOy�еĵ�P�͡�C���������¶��壺�����ڹ���P��ֱ��l����C�����ڵ�P��A��B���㣬��P��A��B�����У�λ���м�ĵ�ǡΪ����������Ϊ�˵���߶ε��е�ʱ����Ƶ�PΪ��C �����ڵ㣬ֱ��lΪ��C���ڵ�P�������ߣ�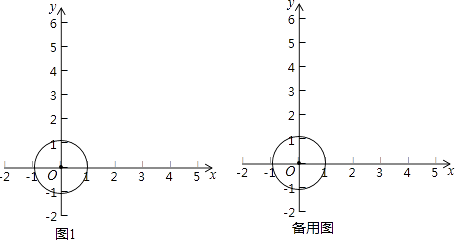
��1������O�İ뾶Ϊ1ʱ��
�ٷֱ��ж��ڵ�D�� ![]() ��
�� ![]() ����E��0����
����E��0���� ![]() ����F��4��0���У��ǡ�O�����ڵ�����
����F��4��0���У��ǡ�O�����ڵ�����
����Ӣ��еĴ��У���ѡһ�����ڵ㣬��ͼ1��������O��������һ�������ߣ���˵�������ͼ���̣�
�۵�P��ֱ��y=��x+3�ϣ�����PΪ��O�����ڵ㣬���P�������ȡֵ��Χ��
��2����C��Բ����x���ϣ��뾶Ϊ1��ֱ��y=�� ![]() ��x�ᣬy��ֱ��ڵ�M��N�����߶�MN�ϴ��ڡ�C�����ڵ�P��ֱ��д��Բ��C�ĺ������ȡֵ��Χ��
��x�ᣬy��ֱ��ڵ�M��N�����߶�MN�ϴ��ڡ�C�����ڵ�P��ֱ��д��Բ��C�ĺ������ȡֵ��Χ��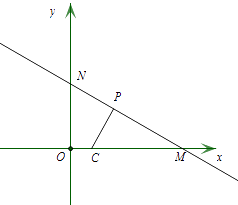
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������M��O��N��Ӧ�����ֱ�Ϊ��2��0��4����PΪ����������һ�㣬���Ӧ����Ϊx��
��1�������P����M��N�ľ�����ȣ���x���� ����
��2���������Ƿ���ڵ�P��ʹ��P����M����N�ľ���֮����10�������ڣ����x��ֵ���������ڣ���˵�����ɣ�
��3�������P��ÿ����1����λ���ȵ��ٶȴӵ�O�����˶���ͬʱ��M�͵�N�ֱ���ÿ����2����λ���Ⱥ�ÿ����3����λ���ȵ��ٶ�Ҳ�����˶�����t����ʱ��P����M����N�ľ�����ȣ���t��ֵ��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
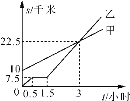
����Ŀ����ͼ���ֱ��ʾ�ײ������������г�(��ͬһ·��)���ߵ�·��s����s����ʱ��t�Ĺ�ϵ���۲�ͼ�ش��������⣺
(1)�ҳ���ʱ���������� ǧ�ף�
(2)����һ��·�̺��ҵ����г��������ϣ�ͣ��������ʱ��Ϊ Сʱ��
(3)�Ҵӳ����𣬾��� Сʱ���������
(4)�������г�������ǰ���ٶ���������ٶ�һ����Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
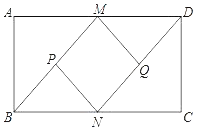
����Ŀ����֪����ͼ���ھ���ABCD�У�M��N�ֱ���AD��BC���е㣬P��Q�ֱ���BM��DN���е㣮
��1����֤��BM��DN��
��2����֤���ı���MPNQ�����Σ�
��3������ABCD�ı߳�AB��AD����ʲô������ϵʱ�ı���MPNQΪ�����Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com