
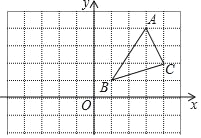
【题目】△ABC在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.
(1)作出△ABC关于y轴对称的△A1B1C1,并写出点C1的坐标 ;
(2)在(1)的条件下,连接CC1交AB于点D,请标出点D,并直接写出CD的长.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如右图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移4格.

(1)请在图中画出平移后的△ABC
(2)再在图中画出△ABC的高CD
(3)![]() =
=
(4)在右图中能使![]() 的格点P的个数有 个(点P异于A) .
的格点P的个数有 个(点P异于A) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张庄甲、乙两家草莓采摘园的草莓销售价格相同,“春节期间”,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为![]() (千克),在甲园所需总费用为
(千克),在甲园所需总费用为![]() (元),在乙园所需总费用为
(元),在乙园所需总费用为![]() (元),
(元),![]() 、
、![]() 与
与![]() 之间的函数关系如图所示,折线OAB表示
之间的函数关系如图所示,折线OAB表示![]() 与
与![]() 之间的函数关系.
之间的函数关系.

(1)甲采摘园的门票是 元,两个采摘园优惠前的草莓单价是每千克 元;
(2)当![]() >10时,求
>10时,求![]() 与
与![]() 的函数表达式;
的函数表达式;
(3)游客在“春节期间”采摘多少千克草莓时,甲、乙两家采摘园的总费用相同.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .
(2)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.
(3)从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
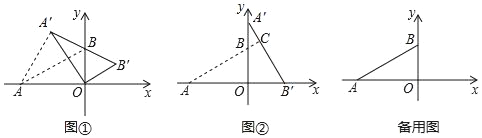
【题目】在平面直角坐标系中,O为原点,点A(﹣![]() ,0),点B(0,1)把△ABO绕点O顺时针旋转,得△A'B'O,点A,B旋转后的对应点为A',B',记旋转角为α(0°<α<360°).
,0),点B(0,1)把△ABO绕点O顺时针旋转,得△A'B'O,点A,B旋转后的对应点为A',B',记旋转角为α(0°<α<360°).
(1)如图①,当点A′,B,B′共线时,求AA′的长.
(2)如图②,当α=90°,求直线AB与A′B′的交点C的坐标;
(3)当点A′在直线AB上时,求BB′与OA′的交点D的坐标(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
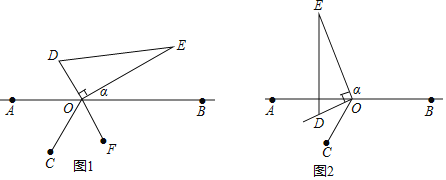
【题目】如图1,点A、O、B在同一直线上,∠AOC=60°,在直线AB另一侧,直角三角形DOE绕直角顶点O逆时针旋转(当OD与OC重合时停止),设∠BOE=α:
(1)如图1,当DO的延长线OF平分∠BOC,∠α=______度;
(2)如图2,若(1)中直角三角形DOE继续逆时针旋转,当OD位于∠AOC的内部,且∠AOD=![]() ∠AOC,∠α=__度;
∠AOC,∠α=__度;
(3)在上述直角三角形DOE的旋转过程中,(∠COD+∠α)的度数是否改变?若不改变,请求出其度数;若改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD的四边都相等,等边△AEF的顶点E、F分别在BC、CD上,且AE=AB,则∠C=( )

A. 100° B. 105° C. 110° D. 120°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com