
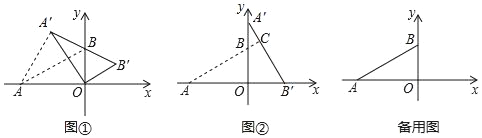
【题目】在平面直角坐标系中,O为原点,点A(﹣![]() ,0),点B(0,1)把△ABO绕点O顺时针旋转,得△A'B'O,点A,B旋转后的对应点为A',B',记旋转角为α(0°<α<360°).
,0),点B(0,1)把△ABO绕点O顺时针旋转,得△A'B'O,点A,B旋转后的对应点为A',B',记旋转角为α(0°<α<360°).
(1)如图①,当点A′,B,B′共线时,求AA′的长.
(2)如图②,当α=90°,求直线AB与A′B′的交点C的坐标;
(3)当点A′在直线AB上时,求BB′与OA′的交点D的坐标(直接写出结果即可)
【答案】(1)AA′=![]() ;(2)(
;(2)(![]() ,
,![]() );(3)(
);(3)(![]() ,
,![]() ).
).
【解析】
(1)如图①,只要证明△AOA′是等边三角形即可;
(2)如图②,当α=90°,点A′在y轴上,作CH⊥OA′于H.解直角三角形求出BH,CH即可解决问题;
(3)如图③,设A′B′交x轴于点K.首先证明A′B′⊥x轴,求出OK,A′K即可解决问题;
(1)如图①,
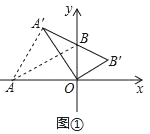
∵A(﹣![]() ,0),B(0,1),
,0),B(0,1),
∴OA=![]() ,OB=1,
,OB=1,
∴tan∠BAO=![]() ,
,
∴∠BAO=30°,∠ABO=60°,
∵△A′OB′是由△AOB旋转得到,
∴∠B′=∠ABO=60°,OB=OB′,OA=OA′,
∴∠OBB′=60°,
∴∠BOB′=α=∠AOA′=60°,
∴△AOA′是等边三角形,
∴AA′=OA=![]() .
.
(2)如图②,当α=90°,点A′在y轴上,作CH⊥OA′于H.
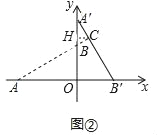
∵∠A′B′O=60°,∠CAB′=30°,
∴∠ACB′=90°,
∵A′B=OA′﹣OB=![]() ﹣1,∠BA′C=30°,
﹣1,∠BA′C=30°,
∴BC=![]() A′B=
A′B=![]() ,
,
∵∠HBC=60°,
∴BH=![]() BC=
BC=![]() ,CH=
,CH=![]() BH=
BH=![]() ,
,
∴OH=1+BH=![]() ,
,
∴点C的坐标(![]() ,
,![]() ).
).
(3)如图③中,设A′B′交x轴于点K.
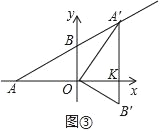
当A′在AB上时,∵OA=OA′,
∴∠OAA′=∠AA′O=30°,
∵∠OA′B′=30°,
∴∠AA′K=60°,
∴∠AKA′=90°,
∵OA′=![]() ,∠OA′K=30°,
,∠OA′K=30°,
∴OK=![]() OA′=
OA′=![]() ,A′K=
,A′K=![]() OK=
OK=![]() ,
,
∴A′(![]() ,
,![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知下列方程:①![]() ;②0.3x=1;③
;②0.3x=1;③![]() ;④x2﹣4x=3;⑤x=6;⑥x+2y=0.其中一元一次方程的个数是( )
;④x2﹣4x=3;⑤x=6;⑥x+2y=0.其中一元一次方程的个数是( )
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AB的中点,点D在线段CB上.
![]()
(1)图中共有 条线段.
(2)图中AD=AC+CD,BC=AB﹣AC,类似地,请你再写出两个有关线段的和与差的关系式:
① ;② .
(3)若AB=8,DB=1.5,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图象(折线OEFPMN)描述了某汽车在行驶过程中速度与时间的函数关系,下列说法中错误的是( )

A. 第3分时汽车的速度是40千米/时
B. 第12分时汽车的速度是0千米/时
C. 从第3分到第6分,汽车行驶了120千米
D. 从第9分到第12分,汽车的速度从60千米/时减少到0千米/时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.
(1)求证:四边形ABEF为菱形;
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
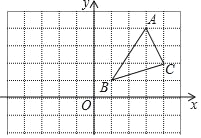
【题目】△ABC在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.
(1)作出△ABC关于y轴对称的△A1B1C1,并写出点C1的坐标 ;
(2)在(1)的条件下,连接CC1交AB于点D,请标出点D,并直接写出CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AE是△ABC的外角∠CAD的平分线.
(1)若AE∥BC,如图1,试说明∠B=∠C;
(2)若AE交BC的延长线于点E,如图2,直接写出反应∠B、∠ACB、∠AEC之间关系的等式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光合作用是指绿色植物通过叶绿体,利用光能,把二氧化碳和水转化成储存能量的有机物,并释放出氧气的过程.如图是夏季的白天7时~18时的一般的绿色植物的光合作用强度与时间之间的关系的曲线,分析图象回答问题:
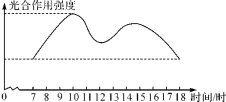
(1)大约几时的光合作用最强?大约几时的光合作用最弱?
(2)说一说绿色植物光合作用的强度从7时到18时是怎样变化的.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com